
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线斜率为1,求函数
处的切线斜率为1,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上单调递增;(2)
上单调递增;(2)![]() .
.
【解析】试题分析:(1)求出![]() ,由
,由![]() ,∴
,∴![]() ,令
,令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)
的减区间;(2)![]() 时,
时,![]() 恒成立等价于
恒成立等价于![]() 恒成立,讨论
恒成立,讨论![]() 、
、![]() ,两种情况,分别利用导数研究函数的单调性,求出函数的最小值,解不等式即可的结果.
,两种情况,分别利用导数研究函数的单调性,求出函数的最小值,解不等式即可的结果.
试题解析:(1)∵ ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴ ![]() ,记
,记![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单减;
单减;
当![]() 时,
时,![]() ,
, ![]() 单增,
单增,
∴![]() ,
,
故![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增
上单调递增
(2)∵![]() ,令
,令![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单增,∴
上单增,∴![]() .
.
ⅰ)当![]() 即
即![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ,∴
,∴![]() 在
在![]() 上单增,
上单增,
∴![]() ,
,![]() ,所以
,所以![]() .
.
ⅱ)当![]() 即
即![]() 时,∵
时,∵![]() 在
在![]() 上单增,且
上单增,且![]() ,
,
当 ![]() 时,
时,![]() ,
,
∴![]() 使
使![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,即
,即![]() 单减;
单减;
当![]() 时,
时,![]() ,即
,即![]() 单增.
单增.
∴![]()
![]() ,
,
∴![]() ,
,![]() ,由
,由![]() ,∴
,∴![]() .
.
记![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() .
.
综上![]() .
.


科目:高中数学 来源: 题型:
【题目】请认真阅读下列程序框图,然后回答问题,其中n0∈N. 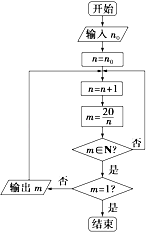
(1)若输入n0=0,写出所输出的结果;
(2)若输出的结果中有5,求输入的自然数n0的所有可能的值;
(3)若输出的结果中,只有三个自然数,求输入的自然数n0的所有可能的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f(
的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f( ![]() )=
)= ![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(x2﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2. 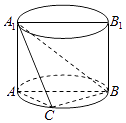
(1)求证:平面AA1C⊥平面BA1C;
(2)若AC=BC,求几何体A1﹣ABC的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x2﹣2ax+3).
(x2﹣2ax+3).
(1)若f(x)的定义域为R,求a的取值范围;
(2)若f(﹣1)=﹣3,求f(x)单调区间;
(3)是否存在实数a,使f(x)在(﹣∞,2)上为增函数?若存在,求出a的范围?若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,互相垂直的两条公路AP、AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=36米,AD=20米.记三角形花园AMN的面积为S. (Ⅰ)问:DN取何值时,S取得最小值,并求出最小值;
(Ⅱ)若S不超过1764平方米,求DN长的取值范围.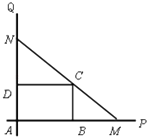
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集有且只有一个元素.
的解集有且只有一个元素.
(1)设数列![]() 的前
的前![]() 项和
项和![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,则数列
,则数列![]() 中是否存在不同的三项
中是否存在不同的三项![]() 成等比数列?若存在,求出这三项,若不存在,请说明理由.
成等比数列?若存在,求出这三项,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)当![]() 时,
时, ![]() ,若当
,若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的图像关于
的图像关于![]() 对称,且
对称,且![]() 时,
时, ![]() ,求当
,求当![]() 时,
时, ![]() 的解析式;
的解析式;
(3)当![]() 时,
时, ![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com