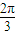【答案】
分析:根据题意画出图形,令直线方程中的x=0,求出y的值,即为|OB|的长;令y=0,求出x的值,即为|OA|的长,在直角三角形AOB中,由|OA|和|OB|的长,利用勾股定理求出|AB|的长,由直角三角形中,一直角边等于斜边的一半得到这条直角边所对的角为30度,进而得到∠ABO=30°,∠BAO=60°,又OA=OC,所以三角形AOC为等边三角形,故∠AOC=60°,由劣弧AC所对的圆心角∠AOC=60°,圆的半径为2,利用弧长公式即可求出劣弧AC的弧长.
解答:解:根据题意画出图形,如图所示:
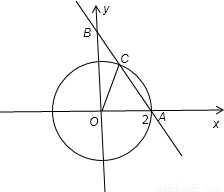
在Rt△AOB中,由|OA|=2,|OB|=2
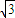
,
根据勾股定理得:|AB|=
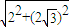
=4,
∵OA=

AB,∴∠OBA=30°,
∴∠BAO=60°,又OA=OC,
∴△AOC为等边三角形,
∴∠AOC=60°,又圆O的半径OA=2,
∴
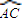
的长度l=
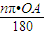
=
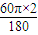
=
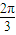
.
故答案为:
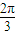 点评:
点评:此题考查了直线与圆相交的性质,直角三角形的性质,等边三角形的判定与性质,以及弧长公式.借助图形找出劣弧所对的圆心角度数是解本题的关键.

 x+y-2
x+y-2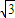 =0截圆x2+y2=4得到的劣弧的弧长为( )
=0截圆x2+y2=4得到的劣弧的弧长为( )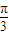



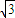 ,
,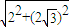 =4,
=4, AB,∴∠OBA=30°,
AB,∴∠OBA=30°,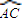 的长度l=
的长度l=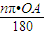 =
=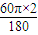 =
=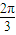 .
.