练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知的三个顶点为， 为的中点.求：

    (1) 所在直线的方程；

    (2) 边上中线所在直线的方程；

    (3) 边上的垂直平分线的方程．

    【答案】（1）x+2y-4=0．（2）2x-3y+6=0．（3）y=2x+2．

    【解析】试题分析：（1）直线方程的两点式求出所在直线的方程；（2）先求BC的中点D坐标为（0,2），由直线方程的截距式求出AD所在直线方程；（3）求出直线)BC的斜率，由两直线垂直的条件求出直线DE的斜率，再由截距式求出DE的方程。

    试题解析：(1)因为直线BC经过B(2，1)和C(-2，3)两点，

    由两点式得BC的方程为y-1= (x-2)，

    即x+2y-4=0．

    (2)设BC中点D的坐标为(x，y)，则x=0，y=2．

    BC边的中线AD过点A(-3，0)，D(0，2)两点，由截距式得

    AD所在直线方程为=1，即2x-3y+6=0．

    (3)BC的斜率，则BC的垂直平分线DE的斜率k2=2，

    由斜截式得直线DE的方程为y=2x+2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x﹣a）（x﹣b）（其中a＞b），若f（x）的图象如图所示，则函数g（x）=ax+b的图象大致为（　　）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知直线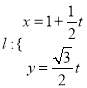（为参数），曲线（为参数）．

    （1）设与相交于两点，求；

    （2）若把曲线上各点的横坐标压缩为原来的倍，纵坐标压缩为原来的倍，得到曲线，设点是曲线上的一个动点，求它到直线的距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段： ， ， ，…后得到如下频率分布直方图.

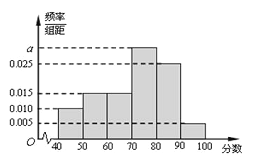
    (1)根据频率分布直方图，估计该校高二年级学生期中考试政治成绩的中位数（精确到0.1）、众数、平均数；

    (2)用分层抽样的方法抽取一个容量为20的样本，求各分数段抽取的人数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图：椭圆与双曲线有相同的焦点、，它们在轴右侧有两个交点、，满足.将直线左侧的椭圆部分（含， 两点）记为曲线，直线右侧的双曲线部分（不含， 两点）记为曲线.以为端点作一条射线，分别交于点，交于点（点在第一象限），设此时.

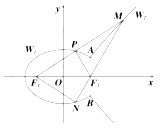
    （1）求的方程；

    （2）证明： ，并探索直线与斜率之间的关系；

    （3）设直线交于点，求的面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在几何体ABDCE中，AB=AD，AE⊥平面ABD，M为线段BD的中点，MC∥AE，AE=MC．
    （1）求证：平面BCD⊥平面CDE；
    （2）若N为线段DE的中点，求证：平面AMN∥平面BEC．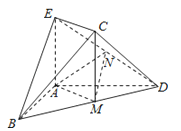

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB为圆柱的轴，CD为底面直径，E为底面圆周上一点，AB=1，CD=2，CE=DE．
    求（1）三棱锥A﹣CDE的全面积；
    （2）点D到平面ACE的距离．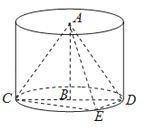

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的顶点， 边上的中线所在直线方程为， 边上的高所在直线方程为．　

    （1）求点的坐标；

    （2）求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知过抛物线焦点且倾斜角的直线与抛物线交于点 的面积为．

    （I）求抛物线的方程；

    （II）设是直线上的一个动点，过作抛物线的切线，切点分别为直线与直线轴的交点分别为点是以为圆心为半径的圆上任意两点，求最大时点的坐标．

    查看答案和解析>>

    同步练习册答案