Question

(理)已知点A(4m,0)、B(m,0)(m是大于0的常数),动点P满足=6m||.

(1)求点P的轨迹C的方程;

(2)点Q是轨迹C上一点,过点Q的直线l交x轴于点F(-m,0),交y轴于点M,若||=2||,求直线l的斜率.

(文)已知椭圆的中心在坐标原点O,焦点在x轴上,左焦点为F,左准线与x轴的交点为M,.

(1)求椭圆的离心率e;

(2)过左焦点F且斜率为的直线与椭圆交于A、B两点,若=-2,求椭圆的方程.

Answer 1

(理)解：(1)设P(x,y),则=(-3m,0),=(x-4m,y),=(m-x,-y).               

∵,

∴-3m(x-4m)=6m.

则点P的轨迹C的方程为=1.                                    

(2)设Q(x_Q,y_Q),直线l:y=k(x+m),则点M(0,km).

当时,由于F(-m,0),M(0,km),得

(x_Q,y_Q-km)=2(-m-x_Q,-y_Q).

x_Q=,y_Q=km.                                                       

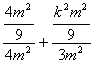又点Q()在椭圆上,所以=1.

解之,得k=±2.                                                          

当时,x_Q=-2m,y_Q=-km.                                          

于是=1,解得k=0.                                             

故直线l的斜率是0,±2.                                                  

(文)解：(1)设椭圆方程为,F(-c,0),M(,0).

由,有(,0)=4(-c,0).                                         

则有=4c,即.

∴e=.                                                              

(2)设直线AB的方程为y=(x+c),直线AB与椭圆的交点为A(x₁,y₁),B(x₂,y₂).

由(1)可得a²=4c²,b²=3c².

由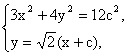

消去y,得11x²+16cx-4c²=0.                                                   

x₁+x₂=,x₁x₂=c².

=(x₁,y₁)·(x₂,y₂)=x₁x₂+y₁y₂,

且y₁·y₂=2(x₁+c)(x₂+c)=2x₁x₂+2c(x₁+x₂)+2c².

∴3x₁x₂+2c(x₁+x₂)+2c²=-2,                                                   

即c²+2c²=-2.

∴c²=1.则a²=4,b²=3.

椭圆的方程为=1.