
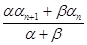 ,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
,n∈N*,其中常数α,β均为非零实数,且α+β≠0.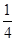 , a1=1,a2=
, a1=1,a2=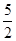 ,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+
,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+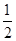 } (n∈N*)中没有相同数值的项.
} (n∈N*)中没有相同数值的项. 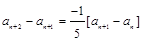 ,可知数列
,可知数列 (n∈N*)为等比数列,进而得到
(n∈N*)为等比数列,进而得到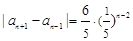 ,然后结合指数函数性质来得到。
,然后结合指数函数性质来得到。 ,
, .
. ,则有
,则有 ,得
,得 ,所以
,所以 为等差数列. 4分
为等差数列. 4分 为非常数等差数列,可令
为非常数等差数列,可令 (k≠0). 代入
(k≠0). 代入 ,得
,得 .
.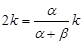 ,即
,即 .
. 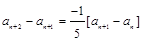 . 10分
. 10分 ,可知数列
,可知数列 (n∈N*)为等比数列,所以
(n∈N*)为等比数列,所以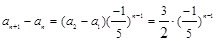 (n∈N*).
(n∈N*). ,
,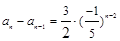 .
.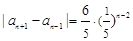 (
( ). 12分
). 12分 ·
· ≤
≤ ·
·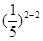 =
= .
. 中项均小于等于
中项均小于等于 .
.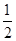 ≥1+
≥1+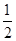 >
> ,所以数列{n+
,所以数列{n+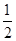 }(n∈N*)中项均大于
}(n∈N*)中项均大于 .
. 与数列{n+
与数列{n+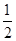 }(n∈N*)中没有相同数值的项.
}(n∈N*)中没有相同数值的项.

科目:高中数学 来源:不详 题型:解答题
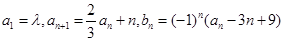 ,其中λ为实数,n为正整数.
,其中λ为实数,n为正整数.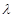 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com