
设函数 对任意
对任意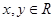 ,都有
,都有 ,当
,当 时,
时,
(1)求证: 是奇函数;
是奇函数;
(2)试问:在 时
时  ,
, 是否有最大值?如果有,求出最大值,如果没有,说明理由.
是否有最大值?如果有,求出最大值,如果没有,说明理由.
(3)解关于x的不等式
(1)详见解析;(2)函数最大值为 ;(3)①
;(3)① ,则解为
,则解为 ;②
;② ,则解为
,则解为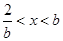 ;③
;③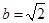 ,则无解.
,则无解.
解析试题分析:(1)要证明 为奇函数,需要证明
为奇函数,需要证明 .如何利用所给条件变出这样一个等式来?
.如何利用所给条件变出这样一个等式来?
为了产生 ,令
,令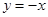 ,则
,则 .这时的
.这时的 等于0吗?如何求
等于0吗?如何求 ?再设
?再设 可得
可得 ,从而问题得证.
,从而问题得证.
(2)一个连续函数在闭区间上必最大值的最小值.为了求函数的最值,就需要研究函数的单调性.研究单调性,第一,根据定义,第二利用导数.抽象函数研究单调性只能用定义.任取 ,则
,则 ,根据条件可得:
,根据条件可得: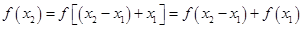 即
即
所以 为减函数,那么函数在
为减函数,那么函数在 上的最大值为
上的最大值为 .
.
(3)有关抽象函数的不等式,都是利用单调性去掉 .首先要将不等式化为
.首先要将不等式化为 ,注意必须是左右各一项.在本题中,由题设可得
,注意必须是左右各一项.在本题中,由题设可得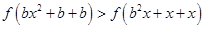 ,
,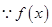 在R上为减函数
在R上为减函数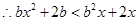 ,即
,即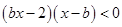 .下面就解这个不等式.这个不等式中含有参数
.下面就解这个不等式.这个不等式中含有参数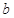 ,故需要分情况讨论.
,故需要分情况讨论.
试题解析:(1)设 可得
可得 ,设
,设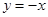 ,则
,则
所以 为奇函数.
为奇函数.
(2)任取 ,则
,则 ,又
,又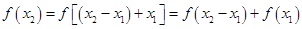
所以
所以 为减函数。
为减函数。
那么函数最大值为 ,
, ,
,
所以函数最大值为 .
.
(3)由题设可知
即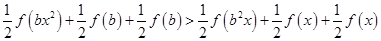
可化为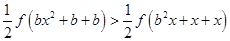
即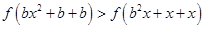 ,
,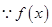 在R上为减函数
在R上为减函数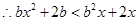 ,即
,即 ,
,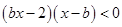
① ,则解为
,则解为
② ,则解为
,则解为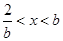
③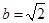 ,则无解
,则无解
考点:1、抽象函数;2、函数的性质;3、解不等式.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,都有
,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,且对任意的
,且对任意的 ,都存在
,都存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度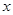 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当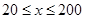 时,车流速度
时,车流速度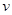 是车流密度x的一次函数.
是车流密度x的一次函数.
(1)当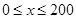 时,求函数
时,求函数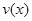 的表达式;
的表达式;
(2)当车流密度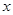 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)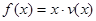 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 在区间
在区间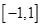 上是增函数.
上是增函数.
(1)求实数 的值组成的集合
的值组成的集合 ;
;
(2)设关于 的方程
的方程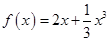 的两个非零实根为
的两个非零实根为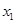 、
、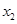 .试问:是否存在实数
.试问:是否存在实数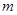 ,使得不等式
,使得不等式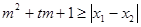 对任意
对任意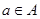 及
及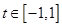 恒成立?若存在,求
恒成立?若存在,求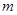 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)是定义在[-3,3]上的奇函数,且当x∈[0,3]时,f(x)=x|x-2|
⑴在平面直角坐标系中,画出函数f(x)的图象
⑵根据图象,写出f(x)的单调增区间,同时写出函数的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com