已知{an}是公差为d的等差数列,{bn}是公比为q的等比数列,设m,n,p,k都是正整数.
(1)求证:若m+n=2p,则am+an=2ap,bmbn=(bp)2;
(2)若an=3n+1,是否存在m,k,使得am+am+1=ak?请说明理由;
(3)求使命题P:“若bn=aqn(a、q为常数,且aq≠0)对任意m,都存在k,有bmbm+1=bk”成立的充要条件.
解:(1)∵{a
n}是公差为d的等差数列,
∴a
m=a
1+(m-1)d,a
n=a
1+(n-1)d,a
m+a
n=2a
1+(m+n-2)d,
又m+n=2p,∴a
m+a
n=2a
1+2(p-1)d,
∵a
1+(p-1)d=a
p,∴a
m+a
n=2a
p. …(3分)
∵{b
n}是公比为q的等比数列,
∴b
m=b
1q
m-1,b
n=b
1q
n-1,b
mb
n=b
12q
m+n-2,
∵m+n=2p,
∴b
mb
n=b
12q
2p-2=b
1q
p-1•b
1q
p-1=b
p•b
p=b
p2. …(6分)
(2)假设存在m,k,使得a
m+a
m+1=a
k,由a
m+a
m+1=a
k得6m+5=3k+1,
即
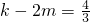
Qm、k∈N
*,∴k-2m为整数,矛盾.∴不存在m、k∈N
+,使等式成立.(10分)
(3)“若b
n=aq
n(a、q为常数,且aq≠0)对任意m,都存在k,有b
mb
m+1=b
k”成立,取m=1,
得b
1b
2=b
k,∴a
2q
3=aq
k,∴a=q
k-3,即a=q
c,其中c是大于等于-2的整数.(13分)
反之,当a=q
c(c是大于等于-2的整数)时,有b
n=q
n+c,
显然b
m?b
m+1=q
m+c?q
m+1+c=q
2m+1+2c=b
k,其中k=2m+1+c.
∴所求的充要条件是a=q
c,其中c是大于等于-2的整数.…(16分)
分析:(1)根据等差数列、等比数列的通项公式即可证得;
(2)由a
m+a
m+1=a
k,得6m+5=3k+1,
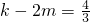
,由m、k∈N
*,知k-2m为整数,所以不存在m、k∈N
*,使等式成立.
(3)“若b
n=aq
n(a、q为常数,且aq≠0)对任意m,都存在k,有b
mb
m+1=b
k”成立,取m=1,可得a=q
c,其中c是大于等于-2的整数,再说明反之也成立,从而得结论.
点评:本题以等差数列、等比数列为载体,考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.

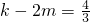
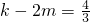 ,由m、k∈N*,知k-2m为整数,所以不存在m、k∈N*,使等式成立.
,由m、k∈N*,知k-2m为整数,所以不存在m、k∈N*,使等式成立. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案