
【题目】设函数f(x)=ax﹣a﹣x(a>0且a≠1)
(1)若f(1)<0,求a的取值范围;
(2)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2mf(x)且g(x)在[1,+∞)上的最小值为﹣2,求m的值.
,g(x)=a2x+a﹣2x﹣2mf(x)且g(x)在[1,+∞)上的最小值为﹣2,求m的值.
【答案】
(1)解:f(x)=ax﹣a﹣x(a>0且a≠1),
∵f(1)<0,
∴a﹣ ![]() <0,
<0,
又a>0,且a≠1,
∴0<a<1
(2)解:∵f(1)= ![]() ,∴a﹣
,∴a﹣ ![]() =
= ![]() ,即2a2﹣3a﹣2=0,
,即2a2﹣3a﹣2=0,
∴a=2或a=﹣ ![]() (舍去)
(舍去)
∴g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2
令t=f(x)=2x﹣2﹣x,
则f(x)=2x﹣2﹣x为增函数,
∵x≥1,
∴t≥f(1)= ![]() ,
,
令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2 (t≥ ![]() )
)
若m≥ ![]() ,当t=m时,h(t)min=2﹣m2=﹣2,∴m=2
,当t=m时,h(t)min=2﹣m2=﹣2,∴m=2
若m< ![]() ,当t=
,当t= ![]() 时,h(t)min=
时,h(t)min= ![]() ﹣3m=﹣2,解得m=
﹣3m=﹣2,解得m= ![]() >
> ![]() ,舍去
,舍去
综上可知m=2
【解析】(1)根据f(1)<0,解不等式可得a的取值范围.(2)根据f(1)= ![]() 确定a=2的值,从而可得函数g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x , 由(1)可知f(x)=2x﹣2﹣x为增函数,可得t≥f(1)=
确定a=2的值,从而可得函数g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x , 由(1)可知f(x)=2x﹣2﹣x为增函数,可得t≥f(1)= ![]() ,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2 (t≥
,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2 (t≥ ![]() ),分类讨论,利用最小值为﹣2,可求m的值
),分类讨论,利用最小值为﹣2,可求m的值
【考点精析】本题主要考查了函数的最值及其几何意义和指、对数不等式的解法的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;指数不等式的解法规律:根据指数函数的性质转化;对数不等式的解法规律:根据对数函数的性质转化才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+lnx(a∈R).
(1)当a=![]() 时,求f(x)在区间[1,e]上的最大值和最小值;
时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f1(x),f2(x),在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“活动函数”.已知函数![]() .
. ![]() 。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 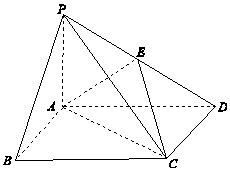
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求二面角D﹣AE﹣C的大小.
,求二面角D﹣AE﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+φ)(ω>0),x=﹣ ![]() 是y=f(x)的零点,直线x=
是y=f(x)的零点,直线x= ![]() 为y=f(x)图象的一条对称轴,且函数f(x)在区间(
为y=f(x)图象的一条对称轴,且函数f(x)在区间( ![]() ,
, ![]() )上单调,则ω的最大值是( )
)上单调,则ω的最大值是( )
A.9
B.7
C.5
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
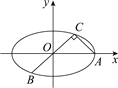
【题目】已知A,B,C是椭圆C: ![]() (a>b>0)上的三点,其中点A的坐标为(2
(a>b>0)上的三点,其中点A的坐标为(2![]() ,0),BC过椭圆的中心,且
,0),BC过椭圆的中心,且![]() ·
·![]() =0,|
=0,|![]() |=2|
|=2|![]() |
|
(1)求椭圆C的方程;
(2)过点(0,t)的直线l(斜率存在)与椭圆C交于P,Q两点,设D为椭圆C与y轴负半轴的交点,且|![]() |=|
|=|![]() |,求实数t的取值范围.
|,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0,
=1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0, ![]() ),则e的取值范围是 .
),则e的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
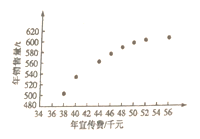
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
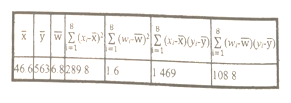
表中![]() .
.
(1)根据散点图判断![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归类型?(给出判断即可,不必说明理由)
的回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的利润![]() 与
与![]() 的的关系为
的的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
(ⅰ)年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的的斜率和截距的最小二乘估计为
的的斜率和截距的最小二乘估计为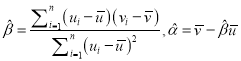 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在![]() 中,斜边
中,斜边![]() ,将
,将![]() 沿直线
沿直线![]() 旋转得到
旋转得到![]() ,设二面角
,设二面角![]() 的大小为
的大小为![]() .
.
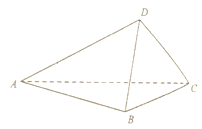
(1)取![]() 的中点
的中点![]() ,过点
,过点![]() 的平面与
的平面与![]() 分别交于点
分别交于点![]() ,当平面
,当平面![]() 平面
平面![]() 时,求
时,求![]() 的长(2)当
的长(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com