
【题目】已知函数![]() ,其中
,其中![]() .
.
![]() Ⅰ
Ⅰ![]() 如果曲线
如果曲线![]() 与x轴相切,求a的值;
与x轴相切,求a的值;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,证明:
,证明:![]() ;
;
![]() Ⅲ
Ⅲ![]() 如果函数
如果函数![]() 在区间
在区间![]() 上不是单调函数,求a的取值范围.
上不是单调函数,求a的取值范围.
【答案】(Ⅰ)1(Ⅱ)详见解析(Ⅲ)(![]() -ln2,1)
-ln2,1)
【解析】
(Ⅰ)先求导,再根据导数的几何意义即可求出,
(Ⅱ)构造函数F(x)=f(x)-x=lnx-2x+ln2e,根据导数和函数单调性的关系以及最值得关系,即可证明
(Ⅲ)先求出函数g(x)在(1,e)上是单调函数a的范围即可,求导,分离参数构造函数,求出函数的最值即可.
解:(I)求导.得f′(x)=![]() -1=
-1=![]()
∵曲线y=f(x)与x轴相切,∴此切线的斜率为0.
由f′(x)=0,解得x=1,
又由曲线y=(x)与x轴相切,得f(1)=-1+a=0
解得a=1.
(II)证明:由题意,f(x)=lnx-x+ln2e,
令函数F(x)=f(x)-x=lnx-2x+ln2e
求导,得F′(x)=![]() -2=
-2=![]()
由F′(x)=0,得x=![]() ,
,
当x变化时,F′(x)与F(x)的变化情况如下表所示:
x | (0, |
| ( |
F′(x) | + | 0 | - |
F(x) | 增 | 极大值 | 减 |
∴函数F(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)单调递减,
,+∞)单调递减,
故当x=![]() 时,F(x)max=F(
时,F(x)max=F(![]() )=ln
)=ln![]() -1+ln2e=0,
-1+ln2e=0,
∴任给x∈(0,+∞),F(x)=f(x)-x≤0,即f(x)≤x,
(Ⅲ)由题意可得,g(x)=![]() ,
,
∴g′(x)=![]() ,
,
当g′(x)≥0时,在(1,e)上恒成立,函数g(x)单调递增,
当g′(x)≤0时,在(1,e)上恒成立,函数g(x)单调递减,
∴x-2lnx+1-2a≥0在(1,e)上恒成立,或x-2lnx+1-2a≤0在(1,e)上恒成立,
∴2a≤x-2lnx+1在(1,e)上恒成立,或2a≥x-2lnx+1在(1,e)上恒成立,
令h(x)=x-2lnx+1,
∴h′(x)=1-![]() =
=![]() ,
,
由h′(x)=0,解得x=2,
当x∈(1,2)时,h′(x)<0,函数h(x)单调递减,
当x∈(2,e)时,h′(x)>0,函数h(x)单调递增,
∵h(1)=2,h(e)=e-2+1=e-1,
∴h(x)max=h(1)=2
∴h(x)min=h(2)=3-2ln2,
∴2a≥2或2a≤3-2ln2,
∴a≥1或a<![]() -ln2,
-ln2,
∵函数![]() 在区间(1,e)上不是单调函数,
在区间(1,e)上不是单调函数,
∴![]() -ln2<a<1,
-ln2<a<1,
故a的取值范围为(![]() -ln2,1).
-ln2,1).


科目:高中数学 来源: 题型:
【题目】小明口袋中有3张10元,3张20元(因纸币有编号认定每张纸币不同),现从中掏出纸币超过45元的方法有_______种;若小明每次掏出纸币的概率是等可能的,不放回地掏出4张,刚好是50元的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在 △ABC 中,设 a,b,c 分别是角 A,B,C 的对边,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产产品x件的总成本c(x)=1200+![]() x3(万元),已知产品单价P(万元)与产品件数x满足:p2=
x3(万元),已知产品单价P(万元)与产品件数x满足:p2=![]() ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为x件时,总利润为L(x)(万元),求L(x)的解析式;
(2)产量x定为多少件时总利润L(x)(万元)最大?并求最大值(精确到1万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
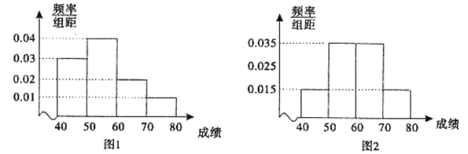
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若幂函数![]() 的图象过点
的图象过点![]() ,则
,则![]()
B.命题![]() :“
:“![]() ,
,![]() ”,则
”,则![]() 的否定为“
的否定为“![]() ,
,![]() ”
”
C.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
D.若![]() 与
与![]() 是相互独立事件,则
是相互独立事件,则![]() 与
与![]() 也是相互独立事件
也是相互独立事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com