
【题目】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.

【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】分析:(Ⅰ)由面面垂直的性质定理可得AD⊥平面ABC,则AD⊥BC.
(Ⅱ)取棱AC的中点N,连接MN,ND.由几何关系可知∠DMN(或其补角)为异面直线BC与MD所成的角.计算可得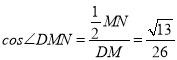 .则异面直线BC与MD所成角的余弦值为
.则异面直线BC与MD所成角的余弦值为![]() .
.
(Ⅲ)连接CM.由题意可知CM⊥平面ABD.则∠CDM为直线CD与平面ABD所成的角.计算可得![]() .即直线CD与平面ABD所成角的正弦值为
.即直线CD与平面ABD所成角的正弦值为![]() .
.
详解:(Ⅰ)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.
(Ⅱ)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.
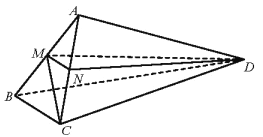
在Rt△DAM中,AM=1,故DM=![]() .因为AD⊥平面ABC,故AD⊥AC.
.因为AD⊥平面ABC,故AD⊥AC.
在Rt△DAN中,AN=1,故DN=![]() .
.
在等腰三角形DMN中,MN=1,可得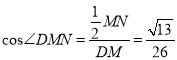 .
.
所以,异面直线BC与MD所成角的余弦值为![]() .
.
(Ⅲ)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=![]() .又因为平面ABC⊥平面ABD,而CM
.又因为平面ABC⊥平面ABD,而CM![]() 平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.
平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.
在Rt△CAD中,CD=![]() =4.
=4.
在Rt△CMD中, ![]() .
.
所以,直线CD与平面ABD所成角的正弦值为![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了
万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:

(1)请判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?
时,日销售额是多少?
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
线性回归方程![]() 中,
中,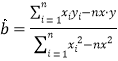 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
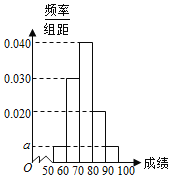
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图![]() 如图所示
如图所示![]() ,规定80分及以上者晋级成功,否则晋级失败.
,规定80分及以上者晋级成功,否则晋级失败.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
![]() Ⅰ
Ⅰ![]() 求图中a的值;
求图中a的值;
![]() Ⅱ
Ⅱ![]() 根据已知条件完成下面
根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“晋级成功”与性别有关?
的把握认为“晋级成功”与性别有关?
![]() Ⅲ
Ⅲ![]() 将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望
将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望![]() 与方差
与方差![]() .
.
![]() 参考公式:
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)试问:函数![]() 的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
(3)若方程![]() 的三个实数根
的三个实数根![]() 、
、![]() 、
、![]() 满足:
满足:![]() <
<![]() <
<![]() ,且
,且![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为
的长度为![]() ,在线段
,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:

记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,现给出有关数列
,现给出有关数列![]() 的四个命题:
的四个命题:
①数列![]() 是等比数列;
是等比数列;
②数列![]() 是递增数列;
是递增数列;
③存在最小的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() ;
;
④存在最大的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() .
.
其中真命题的序号是________________(请写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com