
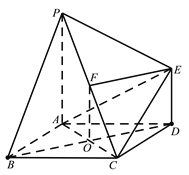
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角
![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,先根据三角形中位线定理及平行四边形的性质可得
,先根据三角形中位线定理及平行四边形的性质可得![]() ,再证明
,再证明![]() 平面
平面![]() ,从而可得
,从而可得![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果
的一个法向量,根据空间向量夹角余弦公式,可得结果
试题解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() .
.
因为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
因为![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]() .
.
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是菱形,所以
是菱形,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解法:因为直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以![]() ,所以
,所以![]() .
.
 所以
所以 ![]() ,故△
,故△![]() 为等边三角形.
为等边三角形.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() .
.
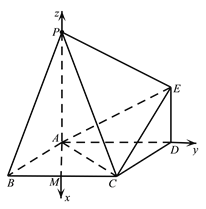
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() (如图).
(如图).
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 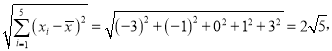 .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 即
即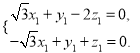
![]() 则
则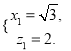 所以
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 即
即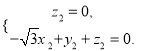 令
令![]() 则
则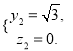 所以
所以![]() .
.
设二面角![]() 的大小为
的大小为![]() ,由于
,由于![]() 为钝角,
为钝角,
所以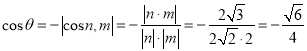 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直及面面垂直的判定定理以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数,据此估计,该运动员三次投篮恰有两次命中的概率为( )
137 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
A.0.40 B.0.30 C.0.35 D.0.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知定圆![]() ,定直线
,定直线![]() ,过
,过![]() 的一条动直线
的一条动直线![]() 与直线相交于
与直线相交于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 中点.
中点.
(Ⅰ)当![]() 与
与![]() 垂直时,求证:
垂直时,求证:![]() 过圆心
过圆心![]() ;
;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)设![]() ,试问
,试问![]() 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出![]() 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,M,N分别为
中,M,N分别为![]() 的中点.
的中点.
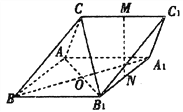
(1)证明:直线MN//平面CAB1;
(2)若四边形ABB1A1是菱形,且![]() ,
, ![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】读下列各题所给的程序,依据程序画出程序框图,并说明其功能:
(1)INPUT “x=”;x
IF x>1 OR x<-1 THEN
y=1
ELSE y=0
END IF
PRINE y
END
(2)INPUT “输入三个正数a,b,c=”;a,b,c
IF a+b>c AND a+c>b AND b+c>a THEN
p=(a+b+c)/2
S=SQR(p*(p-a)*(p-b)*(p-c))
PRINT “三角形的面积S=”S
ELSE
PRINT “构不成三角形”
END IF
END
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,向量
,向量![]() ,
, ![]() ,经过点
,经过点![]() ,以
,以![]() 为方向向量的直线与经过点
为方向向量的直线与经过点![]() ,以
,以![]() 为方向向量的直线交于点
为方向向量的直线交于点![]() ,其中
,其中![]() .
.
(![]() )求点
)求点![]() 的轨迹方程,并指出轨迹
的轨迹方程,并指出轨迹![]() .
.
(![]() )若点
)若点![]() ,当
,当![]() 时,
时, ![]() 为轨迹
为轨迹![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com