
【题目】已知椭圆![]() :
:![]() ,
,![]() ,
,![]() 分别是椭圆短轴的上下两个端点,
分别是椭圆短轴的上下两个端点,![]() 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点![]() ,
,![]() 的点,若
的点,若![]() 的边长为4的等边三角形.
的边长为4的等边三角形.
![]() 写出椭圆的标准方程;
写出椭圆的标准方程;
![]() 当直线
当直线![]() 的一个方向向量是
的一个方向向量是![]() 时,求以
时,求以![]() 为直径的圆的标准方程;
为直径的圆的标准方程;
![]() 设点R满足:
设点R满足:![]() ,
,![]() ,求证:
,求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
![]() 由
由![]() 是边长为4的等边三角形得
是边长为4的等边三角形得![]() ,进一步求得
,进一步求得![]() ,则椭圆方程可求;
,则椭圆方程可求;
![]() 由直线
由直线![]() 的一个方向向量是
的一个方向向量是![]() ,可得直线
,可得直线![]() 所在直线的斜率
所在直线的斜率![]() ,得到直线
,得到直线![]() 的方程,由椭圆方程联立,求得P点坐标,得到
的方程,由椭圆方程联立,求得P点坐标,得到![]() 的中点坐标,再求出
的中点坐标,再求出![]() ,可得以
,可得以![]() 为直径的圆的半径,则以
为直径的圆的半径,则以![]() 为直径的圆的标准方程可求;
为直径的圆的标准方程可求;
![]() 方法一、设
方法一、设![]() ,
,![]() 求出直线
求出直线![]() 的斜率,进一步得到直线
的斜率,进一步得到直线![]() 的斜率,得到直线
的斜率,得到直线![]() 的方程,同理求得直线
的方程,同理求得直线![]() 的方程,联立两直线方程求得R的横坐标,再结合
的方程,联立两直线方程求得R的横坐标,再结合![]() 在椭圆
在椭圆![]() 上可得
上可得![]() 与
与![]() 的关系,由
的关系,由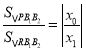 求解;
求解;
方法二、设直线![]() ,
,![]() 的斜率为k,得直线
的斜率为k,得直线![]() 的方程为
的方程为![]() 结合
结合![]() ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,把
,把![]() 与椭圆方程联立可得
与椭圆方程联立可得![]() ,再由
,再由![]() 在椭圆
在椭圆![]() 上,得到
上,得到![]() ,从而得到
,从而得到![]() ,得
,得![]() 结合
结合![]() ,可得直线
,可得直线![]() 的方程为
的方程为![]() 与线
与线![]() 的方程联立求得
的方程联立求得![]() 再由
再由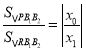 求解.
求解.
![]() 解:如图,由
解:如图,由![]() 的边长为4的等边三角形,得
的边长为4的等边三角形,得![]() ,且
,且![]() .
.

![]() 椭圆的标准方程为
椭圆的标准方程为![]() ;
;
![]() 解:
解:![]() 直线
直线![]() 的一个方向向量是
的一个方向向量是![]() ,
,
![]() 直线
直线![]() 所在直线的斜率
所在直线的斜率![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立 ,得
,得![]() ,
,
解得![]() ,
,![]() .
.
则![]() 的中点坐标为
的中点坐标为![]() ,
,![]() .
.
则以![]() 为直径的圆的半径
为直径的圆的半径![]() .
.
![]() 以
以![]() 为直径的圆的标准方程为
为直径的圆的标准方程为![]() ;
;
![]() 证明:方法一、设
证明:方法一、设![]() ,
,![]()
直线![]() 的斜率为
的斜率为![]() ,由
,由![]() ,得直线
,得直线![]() 的斜率为
的斜率为![]() .
.
于是直线![]() 的方程为:
的方程为:![]() .
.
同理,![]() 的方程为:
的方程为:![]() .
.
联立两直线方程,消去y,得![]() .
.
![]() 在椭圆
在椭圆![]() 上,
上,
![]() ,从而
,从而![]() .
.
![]() ,
,
 .
.
方法二、设直线![]() ,
,![]() 的斜率为k,
的斜率为k,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
![]() 是椭圆上异于点
是椭圆上异于点![]() ,
,![]() 的点,
的点,![]() ,从而
,从而![]() .
.
![]() 在椭圆
在椭圆![]() 上,
上,
![]() ,从而
,从而![]() .
.
![]() ,得
,得![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() .
.
联立 ,解得
,解得![]() ,即
,即![]() .
.
 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.

(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过年时小明的舅舅在家庭微信群里发了一个10元的红包,红包被随机分配为2.51元,3.32元,1.24元,0.26元,2.67元,共五份.现已知小明与爸爸都各自抢到了一个红包,则两人抢到红包的金额总和不小于4元的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为鼓励家校互动,与某手机通讯商合作,为教师办理流量套餐.为了解该校教师手机流量使用情况,通过抽样,得到![]() 位教师近
位教师近![]() 年每人手机月平均使用流量
年每人手机月平均使用流量![]() (单位:
(单位:![]() )的数据,其频率分布直方图如下:
)的数据,其频率分布直方图如下:

若将每位教师的手机月平均使用流量分别视为其手机月使用流量,并将频率为概率,回答以下问题.
(Ⅰ) 从该校教师中随机抽取![]() 人,求这
人,求这![]() 人中至多有
人中至多有![]() 人月使用流量不超过
人月使用流量不超过![]()
![]() 的概率;
的概率;
(Ⅱ) 现该通讯商推出三款流量套餐,详情如下:
套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位: |
|
|
|
|
|
|
|
|
|
这三款套餐都有如下附加条款:套餐费月初一次性收取,手机使用一旦超出套餐流量,系统就自动帮用户充值![]()
![]() 流量,资费
流量,资费![]() 元;如果又超出充值流量,系统就再次自动帮用户充值
元;如果又超出充值流量,系统就再次自动帮用户充值![]()
![]() 流量,资费
流量,资费![]() 元/次,依次类推,如果当月流量有剩余,系统将自动清零,无法转入次月使用.
元/次,依次类推,如果当月流量有剩余,系统将自动清零,无法转入次月使用.
学校欲订购其中一款流量套餐,为教师支付月套餐费,并承担系统自动充值的流量资费的![]() ,其余部分由教师个人承担,问学校订购哪一款套餐最经济?说明理由.
,其余部分由教师个人承担,问学校订购哪一款套餐最经济?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛,每比赛一局商家要向每名棋手支付2000元对局费,同时商家每局从转让网络转播权及广告宣传中获利12100元,从两名棋手以往比赛中得知,甲每局获胜的概率为![]() ,乙每局获胜的概率为
,乙每局获胜的概率为![]() ,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
(1)求下完五局且甲获胜的概率是多少;
(2)求商家从这场网络棋赛中获得的收益的数学期望是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com