
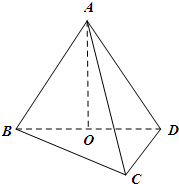
 设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=
设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=| 2 |
| 2 |
| ||
| 2 |
| AC2-OC2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 12 |
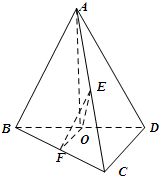 ,取BC中点F,AC中点E,连接EF,OE,OF
,取BC中点F,AC中点E,连接EF,OE,OF| AB |
| 2 |
| ||
| 2 |
| ||||||
| 2 |
| 1 |
| 2 |
| CD |
| 2 |
| ||
| 2 |
| AC |
| 2 |
| ||
| 2 |
| ||||||
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江苏省常州二中2008高考一轮复习综合测试4、数学(文科) 题型:022
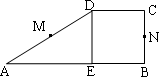
设M、N是直角梯形ABCD两腰的中点,且CD=BC,DE⊥AB于E(如图),现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCD内的射影恰为点B,则M、N的连线与AC所成的角的大小为________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
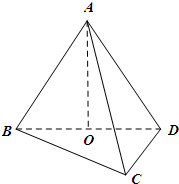 设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=
设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD= .(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.
.(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省雅安市高一(下)期末数学试卷(解析版) 题型:解答题
 .(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.
.(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com