
若函数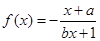 为区间
为区间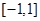 上的奇函数,则它在这一区间上的最大值是 .
上的奇函数,则它在这一区间上的最大值是 .
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:2012届浙江省杭州学军中学高三第一次月考理科数学 题型:解答题
(本小题满分14分)
已知函数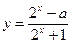 为R上的奇函数
为R上的奇函数
(1)求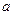 的值
的值
(2)求函数的值域
(3)判断函数的单调区间并证明
查看答案和解析>>
科目:高中数学 来源:2014届重庆市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数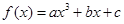 在
在 处取得极值
处取得极值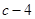 .
.
(1)求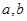 ;
;
(2)设函数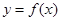 为R上的奇函数,求函数
为R上的奇函数,求函数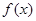 在区间
在区间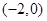 上的极值.
上的极值.
查看答案和解析>>
科目:高中数学 来源:2014届重庆市高二4月月考文科数学试卷(解析版) 题型:解答题
若函数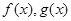 都在区间
都在区间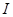 上有定义,对任意
上有定义,对任意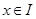 ,都有
,都有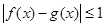 成立,则称函数
成立,则称函数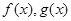 为区间
为区间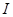 上的“伙伴函数”
上的“伙伴函数”
(1)若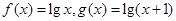 为区间
为区间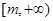 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断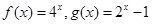 是否为区间
是否为区间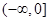 上的“伙伴函数”?
上的“伙伴函数”?
(3)若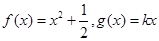 为区间
为区间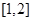 上的“伙伴函数”,求
上的“伙伴函数”,求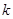 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2014届河南省周口市高一下学期四校第一次联考文科数学试卷(解析版) 题型:选择题
若函数 为R上的奇函数,且在定义域上单调递减,又
为R上的奇函数,且在定义域上单调递减,又 ,
,  ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A.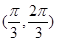 B、
B、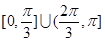
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com