解:(Ⅰ)∵
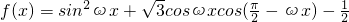
=
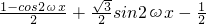
=
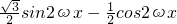
=
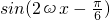
.(2分) 根据题意,
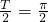
,即T=π,所以
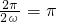
,即ω=1.(4分)
从而
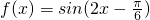
,故
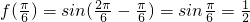
.(6分)
(Ⅱ)因为

,k>0,(8分)
则当
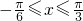
时,
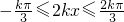
.(9分)
据题意,
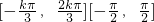
,所以
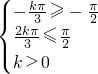
,解得
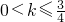
.
故实数k的取值范围是
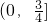
.(12分)
(III)∵
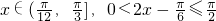
,∴0<f(x)≤1,设f(x)=t,
问题转化为探究是否存在实数m的值使方程3t
2-t+m=0在(0,1]内仅有一根或两个相等实根.(14分)
又∵

,(16分)
所以直线y=m与二次函数y=-3t
2+t,t∈(0,1]的图象有唯一公共点,由图象可知,
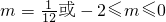
;(19分)
所以实数m的取值范围为
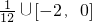
.(20分)
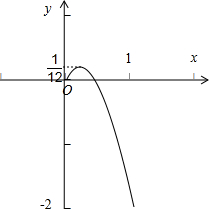
分析:(Ⅰ)利用三角函数的恒等变换化简函数f(x)的解析式为
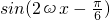
,由此根据它的周期求出ω的值,即可求得
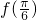
的值.
(Ⅱ)因为
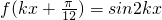
,k>0,则当
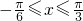
时,
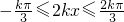
,根据题意得
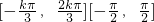
,故
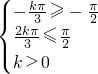
,有此解得实数k的取值范围.
(III)问题转化为探究是否存在实数m的值使方程3t
2-t+m=0在(0,1]内仅有一根或两个相等实根,即直线y=m与二次函数y=-3t
2+t,t∈(0,1]的图象有唯一公共点,由图象可得实数m的取值范围.
点评:本题主要考查三角函数的恒等变换,利用y=Asin(ωx+∅)的图象特征性质的应用,二次函数的性质,体现了数形结合以及等价转化的数学思想,属于中档题.

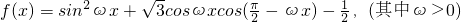 ,且函数y=f(x)的图象相邻两条对称轴之间的距离为
,且函数y=f(x)的图象相邻两条对称轴之间的距离为 .
.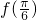 的值;
的值;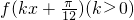 在区间
在区间 上单调递增,求实数k的取值范围;
上单调递增,求实数k的取值范围;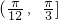 内仅有一解,若存在,求出实数m的取值范围,若不存在,说明理由.
内仅有一解,若存在,求出实数m的取值范围,若不存在,说明理由.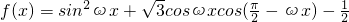 =
=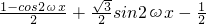
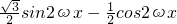 =
=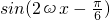 .(2分) 根据题意,
.(2分) 根据题意,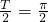 ,即T=π,所以
,即T=π,所以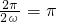 ,即ω=1.(4分)
,即ω=1.(4分)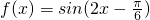 ,故
,故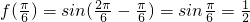 .(6分)
.(6分) ,k>0,(8分)
,k>0,(8分)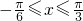 时,
时,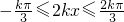 .(9分)
.(9分)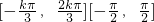 ,所以
,所以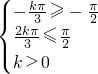 ,解得
,解得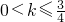 .
.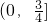 .(12分)
.(12分)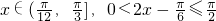 ,∴0<f(x)≤1,设f(x)=t,
,∴0<f(x)≤1,设f(x)=t, ,(16分)
,(16分)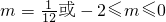 ;(19分)
;(19分)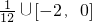 .(20分)
.(20分)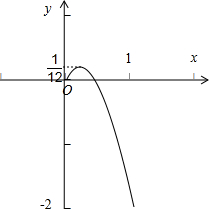
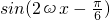 ,由此根据它的周期求出ω的值,即可求得
,由此根据它的周期求出ω的值,即可求得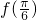 的值.
的值.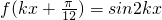 ,k>0,则当
,k>0,则当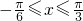 时,
时,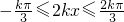 ,根据题意得
,根据题意得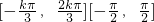 ,故
,故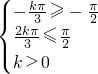 ,有此解得实数k的取值范围.
,有此解得实数k的取值范围.

 阅读快车系列答案
阅读快车系列答案 ,且函数y=f(x)的图象相邻两条对称轴之间的距离为
,且函数y=f(x)的图象相邻两条对称轴之间的距离为 .
. 的值;
的值; 在区间
在区间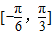 上单调递增,求实数k的取值范围;
上单调递增,求实数k的取值范围; 内仅有一解,若存在,求出实数m的取值范围,若不存在,说明理由.
内仅有一解,若存在,求出实数m的取值范围,若不存在,说明理由.