
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
【答案】解:由题意:F(x)=f(x)﹣g(x),那么:F(x)=xlnx﹣ ![]() .定义域为(0,+∞)
.定义域为(0,+∞)
F′(x)=1+lnx+ ![]() ,由题设x∈(1,2),故F′(x)>0,即F(x)在区间(1,2)上是增函数.(1,2)是单调增区间.那么:F(1)=ln1﹣
,由题设x∈(1,2),故F′(x)>0,即F(x)在区间(1,2)上是增函数.(1,2)是单调增区间.那么:F(1)=ln1﹣ ![]() =
= ![]() <0,F(2)=2ln2﹣
<0,F(2)=2ln2﹣ ![]() >0,并且F(x)在(1,2)上连续的,故根据零点定理,有F(x)在区间(1,2)有且仅有唯一实根,即一个零点.
>0,并且F(x)在(1,2)上连续的,故根据零点定理,有F(x)在区间(1,2)有且仅有唯一实根,即一个零点.
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , 由f(x)=xlnx,当0<x≤1时,f(x)≤0,而g(x)= ![]() >0,故f(x)<g(x);
>0,故f(x)<g(x);
由(Ⅰ)可知F′(x)=1+lnx+ ![]() ,当x>1时,F′(x)>0,存在零点x0∈(1,2),不然有:F(x0)=f(x0)﹣g(x0)=0,故1<x<x0时,f(x)<g(x);当x>x0时,f(x)>g(x);
,当x>1时,F′(x)>0,存在零点x0∈(1,2),不然有:F(x0)=f(x0)﹣g(x0)=0,故1<x<x0时,f(x)<g(x);当x>x0时,f(x)>g(x);
而此得到m(x)= 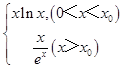 ,
,
显然:当1<x<x0时,m′(x)=1+lnx恒大于0,m(x)是单增函数.
当x>x0时,m′(x)= ![]() 恒小于0,m(x)是单减函数.
恒小于0,m(x)是单减函数.
m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),则x1∈(1,x0),x2∈(x0 , +∞),
显然:当x2→+∞时,x1+x2>2x0 .
要证明x1+x2>2x0 , 即可证明x2>2x0﹣x1>x0 , 而m(x)在x>x0时是单减函数.故证m(x2)<m(2x0﹣x1).
又由m(x1)=m(x2),即可证:m(x1)<m(2x0﹣x1).即x1lnx1< ![]() ,(构造思想)
,(构造思想)
令h(x)=xlnx﹣ ![]() ,由(1<x<x0).其中h(x0)=0,
,由(1<x<x0).其中h(x0)=0,
那么:h′(x)=1+lnx+ ![]() ﹣
﹣ ![]() ,
,
记φ(t)= ![]() ,则φ′(t)=
,则φ′(t)= ![]() ,当t∈(0,1)时,φ′(t)>0;当t>1时,φ′(t)<0;故φ(t)max=
,当t∈(0,1)时,φ′(t)>0;当t>1时,φ′(t)<0;故φ(t)max= ![]() ;
;
而φ(t)>0;故 ![]() >φ(t)>0,而2x0﹣x>0,从而有:
>φ(t)>0,而2x0﹣x>0,从而有: ![]() <0;
<0;
因此:h′(x)=1+lnx+ ![]() ﹣
﹣ ![]() >0,即h(x)单增,从而1<x<x0时,h(x)<h(x0)=0.
>0,即h(x)单增,从而1<x<x0时,h(x)<h(x0)=0.
即x1lnx1< ![]() 成立.
成立.
故得:x1+x2>2x0 .
【解析】(Ⅰ)对F(x)求导,利用x∈(1,2)判定导函数的符号,进而得到函数的单调性,在利用零点存在定理进行证明.(Ⅱ)先由x的范围讨论f(x),g(x)的大小,确定之间的关系式m(x),在判断x1+x2与2x0的大小,可以利用分析法对其进行证明.
【考点精析】本题主要考查了函数的极值与导数和函数的零点与方程根的关系的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.
是极小值;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且cos2 ![]() =
= ![]() ,△ABC的面积为4.
,△ABC的面积为4.
(1)求 ![]() 的值;
的值;
(2)若2sinB=5sinC,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右焦点为
的右焦点为![]() ,
, ![]() 是双曲线C上的点,
是双曲线C上的点, ![]() ,连接
,连接![]() 并延长
并延长![]() 交双曲线C与点P,连接
交双曲线C与点P,连接![]() ,若
,若![]() 是以
是以![]() 为顶点的等腰直角三角形,则双曲线C的渐近线方程为( )
为顶点的等腰直角三角形,则双曲线C的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市自来水公司每两个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过![]() 吨时,按每吨
吨时,按每吨![]() 元收取;当该用户用水量超过
元收取;当该用户用水量超过![]() 吨时,超出部分按每吨
吨时,超出部分按每吨![]() 元收取.
元收取.
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为![]() 元,且甲、乙两用户用水量之比为
元,且甲、乙两用户用水量之比为![]() ,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在约束条件 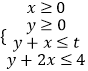 下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
A.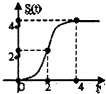
B.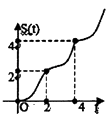
C.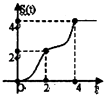
D.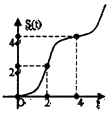
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[﹣ ![]() ,
, ![]() ]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
A.( ![]() ,2]
,2]
B.(﹣∞, ![]() )∪[2,+∞)
)∪[2,+∞)
C.[﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪(
]∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,满足
,满足![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业一天中不同时刻的用电量![]() (万千瓦时)关于时间
(万千瓦时)关于时间![]() (小时,
(小时,![]() )的函数
)的函数![]() 近似满足
近似满足![]() ,如图是函数
,如图是函数![]() 的部分图象(
的部分图象(![]() 对应凌晨
对应凌晨![]() 点).
点).

(Ⅰ)根据图象,求![]() 的值;
的值;
(Ⅱ)由于当地冬季雾霾严重,从环保的角度,既要控制火力发电厂的排放量,电力供应有限;又要控制企业的排放量,于是需要对各企业实行分时拉闸限电措施.已知该企业某日前半日能分配到的供电量![]() (万千瓦时)与时间
(万千瓦时)与时间![]() (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型![]() 模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com