
 中,以
中,以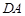 所在直线为
所在直线为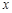 轴,以
轴,以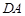 中点
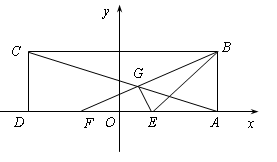
中点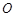 为坐标原点,建立如图所示的平面直角坐标系.已知点
为坐标原点,建立如图所示的平面直角坐标系.已知点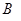 的坐标为
的坐标为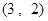 ,E、F为
,E、F为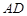 的两个三等分点,
的两个三等分点,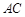 和
和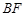 交于点
交于点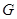 ,
,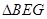 的外接圆为⊙
的外接圆为⊙ .
. 
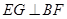 ;
; 的方程;
的方程;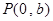 ,过点P作直线与⊙
,过点P作直线与⊙ 交于M,N两点,若点M恰好是线段PN的中点,求实数
交于M,N两点,若点M恰好是线段PN的中点,求实数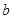 的取值范围.
的取值范围.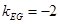 ,
,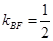 ,根据
,根据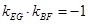 。
。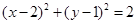 .
. 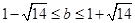 .
.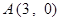 ,
,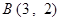 ,
,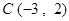 ,
,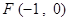 .
.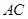 和直线
和直线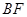 的方程分别为:
的方程分别为: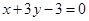 ,
,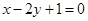 ,
,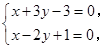 解得
解得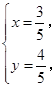 所以
所以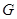 点的坐标为
点的坐标为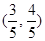 . 6分
. 6分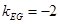 ,
,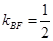 ,
,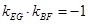 ,所以
,所以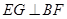 , 8分
, 8分 的圆心为
的圆心为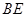 中点
中点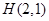 ,半径为
,半径为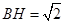 ,
, 方程为
方程为 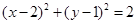 . 10分
. 10分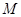 点的坐标为
点的坐标为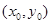 ,则
,则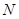 点的坐标为
点的坐标为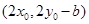 ,
,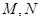 均在⊙
均在⊙ 上,所以
上,所以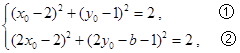 ,
,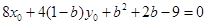 ,
,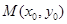 在直线
在直线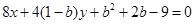 , 12分
, 12分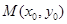 在⊙
在⊙ 上,
上,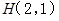 到直线
到直线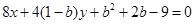 的距离
的距离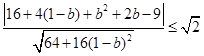
 , 14分
, 14分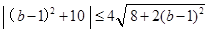 ,
,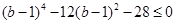 ,即
,即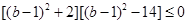 ,
,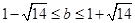 ,故
,故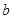 的取值范围为
的取值范围为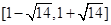 . 16分
. 16分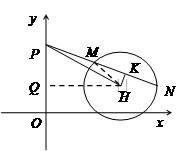
 作
作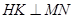 交
交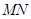 于
于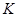 ,
, 到直线
到直线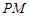 的距离
的距离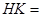
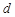 ,则
,则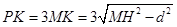 ,
,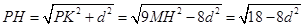 ,
,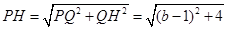
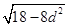
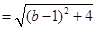 ,
,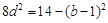 ,因为
,因为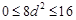 ,
,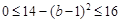 ,所以
,所以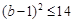 ,
,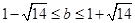 ;
;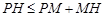 ,
,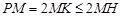 ,所以
,所以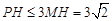
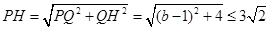 ,所以
,所以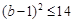 ,
,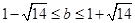 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com