
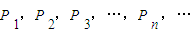 ,已知当n≥2时,点
,已知当n≥2时,点 是把线段
是把线段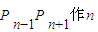 等分的分点中最靠近
等分的分点中最靠近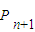 的点,设线段
的点,设线段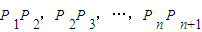 的长度分别为
的长度分别为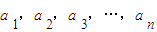 ,其中
,其中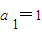 .
.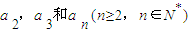 的表达式;
的表达式;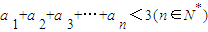 ;
;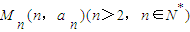 ,在这些点中是否存在两个点同时在函数
,在这些点中是否存在两个点同时在函数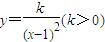 的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.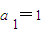 ,代入即可求解
,代入即可求解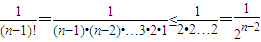 ,利用放缩法,结合等比数列的求和公式可证
,利用放缩法,结合等比数列的求和公式可证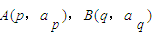 都在函数
都在函数 的图象上,把点的 坐标代入可得
的图象上,把点的 坐标代入可得 ,然后进行推理,即可判断
,然后进行推理,即可判断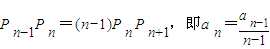 ,
,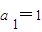 ,
,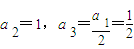 ,
, ,
, .
. ,
,
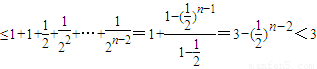
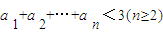 ,
, 显然成立,
显然成立,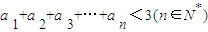 ;
; (其中p≠q,p,q∈N*,p>2,q>2)都在函数
(其中p≠q,p,q∈N*,p>2,q>2)都在函数 的图象上,
的图象上, ,
, ,
, ,
, ,
, 不成立,故不存在满足题设条件的两个点.
不成立,故不存在满足题设条件的两个点.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
| P | 1 |
| P | 2 |
| P | 3 |
| P | n |
| P | n |
| P | n-1 |
| P | n+1 |
| P | n+1 |
| P | 1 |
| P | 2 |
| P | 2 |
| P | 3 |
| P | n |
| P | n+1 |
| a | 1 |
| a | 2 |
| a | 3 |
| a | n |
| a | 1 |
| a | 2 |
| a | 3 |
| a | n |
| a | 1 |
| a | 2 |
| a | 3 |
| a | n |
| M | n |
| a | n |
| k |
| (x-1)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com