
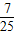 .
.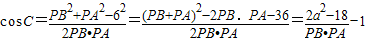 及基本不等式PB.PA
及基本不等式PB.PA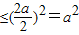 ,可求
,可求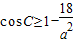 ,从而可求a,及C点的轨迹方程
,从而可求a,及C点的轨迹方程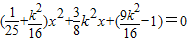 ,显然有△≥0,由椭圆第二定义可得|BM|•|BN|=(5-
,显然有△≥0,由椭圆第二定义可得|BM|•|BN|=(5-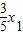 )(5-
)(5-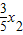 )及方程的根与系数的关系|BM|•|BN|取最小值,结合椭圆的
)及方程的根与系数的关系|BM|•|BN|取最小值,结合椭圆的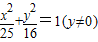 得性质判断M,N是否存在,使得|BM|•|BN|的最小值
得性质判断M,N是否存在,使得|BM|•|BN|的最小值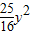 +(y-4)2
+(y-4)2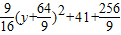 ,由-4≤y≤4且y≠0,结合二次函数的性质可求
,由-4≤y≤4且y≠0,结合二次函数的性质可求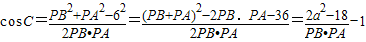 (2分)
(2分)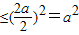 ,
,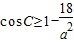 ,此时p(0,±4),由题意得
,此时p(0,±4),由题意得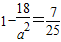
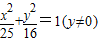 (3分)
(3分)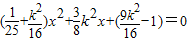 ,显然有△≥0
,显然有△≥0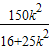 ,x1.x2=
,x1.x2=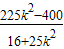
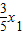 )(5-
)(5-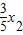 )=25-3(x1+x2)
)=25-3(x1+x2) 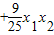 …(2分)
…(2分)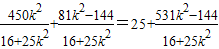
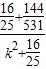 的最小值,即考虑1-
的最小值,即考虑1-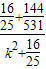 的最小值,易知当k=0时,1-
的最小值,易知当k=0时,1-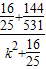 的最小值
的最小值 )2>16;(1分)
)2>16;(1分)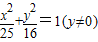 ,故这样的M,N不存在,即|BM|•|BN|的最小值集合为空集(1分)
,故这样的M,N不存在,即|BM|•|BN|的最小值集合为空集(1分)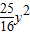 +(y-4)2=-
+(y-4)2=-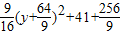 ,
,

科目:高中数学 来源: 题型:
| 7 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 7 |
| 25 |
| BM |
| BN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年湖北补习学校联考理)(14分)在周长为定值的△ABC中,已知|AB|=6,且当顶点C位于定点P时,cosC有最小值为![]() .
.
(Ⅰ)建立适当的坐标系,求顶点C的轨迹方程.
(Ⅱ)过点A作直线与(Ⅰ)中的曲线交于M、N两点,求查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西师大附中高三年级上学期期中考试理科数学试卷(解析版) 题型:解答题
在周长为定值的DDEC中,已知 ,动点C的运动轨迹为曲线G,且当动点C运动时,
,动点C的运动轨迹为曲线G,且当动点C运动时, 有最小值
有最小值 .
.
(1)以DE所在直线为x轴,线段DE的中垂线为y轴建立直角坐标系,求曲线G的方程;
(2)直线l分别切椭圆G与圆 (其中
(其中 )于A、B两点,求|AB|的取值范围.
)于A、B两点,求|AB|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com