
如图,直角三角形PAQ的顶点P(-3,0),点A在y轴上,点Q在x轴正半轴上,∠PAQ=90°.在AQ的延长线上取点M,使![]() .
.
(1)当点A在y轴上移动时,求动点M的轨迹C;
(2)设轨迹C的准线为l,焦点为F,过F作直线m交轨迹C于G、H两点,过点G作平行轨迹C的对称轴的直线n且n∩l=E.试问:点E、O、H(O为坐标原点)是否在同一条直线上?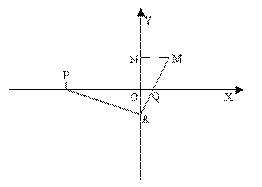 说理由.
说理由.


科目:高中数学 来源: 题型:
 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
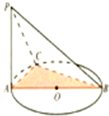 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,则图中直角三角形有
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,则图中直角三角形有查看答案和解析>>
科目:高中数学 来源:江苏省扬州市安宜高中2010-2011学年高二上学期期末考试数学试题 题型:044
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点B(0,-2![]() ),顶点C在x轴上,点P为线段PA的中点.
),顶点C在x轴上,点P为线段PA的中点.
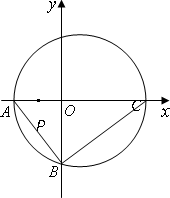
(1)求BC边所在直线方程;
(2)M为直角三角形ABC外接圆的圆心,求圆M的方程;
(3)直线l过点P且倾斜角为![]() ,求该直线被圆M截得的弦长.
,求该直线被圆M截得的弦长.
查看答案和解析>>
科目:高中数学 来源:陕西省模拟题 题型:解答题
 ,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E。
,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E。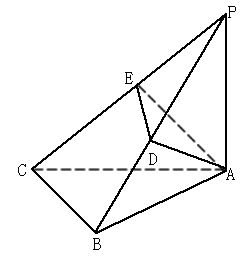
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com