Question

【题目】如图，正三棱柱ABC﹣A1B1C1的各棱长相等，点D是棱CC1的中点，则AA1与面ABD所成角的大小是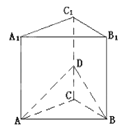

Answer 1

【答案】60°
【解析】解：正三棱柱ABC﹣A1B1C1的各棱长相等，点D是棱CC1的中点，
设棱长为2，以ABC平面内AC顺时针旋转90°得到的直线为x轴，以AC为y轴，以AA1为z轴，
建立如图所示的空间直角坐标系，
则A（0，0，0），B（2sin30°，2sin60°，0）=（ ， 1，0），D（0，2，1），A1（0，0，2），
∴=（0，0，2），=（0，2，1），=（ ， 1，0），
设平面ABD的法向量为=（x，y，z），
则 ，
∴ ， 解得=（ ， ﹣3，6），
设AA1与面ABD所成角为θ，
则．
∴θ=60°．
故AA1与面ABD所成角的大小是60°．
所以答案是：60°．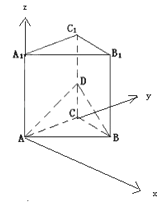

【考点精析】本题主要考查了用空间向量求直线与平面的夹角的相关知识点，需要掌握设直线的方向向量为，平面的法向量为，直线与平面所成的角为，与的夹角为，　则为的余角或的补角的余角.即有：才能正确解答此题．