
(本题共12分)
已知函数 ,其中
,其中 且
且 。
。
(Ⅰ)讨论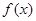 的单调性;
的单调性;
(Ⅱ)求函数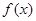 在〔
在〔 ,
, 〕上的最小值和最大值。
〕上的最小值和最大值。
(Ⅰ)函数 在
在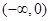 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;
(Ⅱ)
当 时,
时, 在
在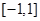 上的最小值为
上的最小值为 ,最大值为
,最大值为 ;
;
当 时,
时, 在
在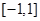 上的最小值为
上的最小值为 ,最大值为
,最大值为
【解析】本试题主要考查了导数研究函数的最值问题的运用。
(1)因为函数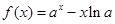 ,其中
,其中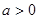 且
且 ,求解导数得到
,求解导数得到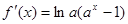 ,然后对于参数a的范围结合对数值来分类讨论得到结论。
,然后对于参数a的范围结合对数值来分类讨论得到结论。
(2)在第一问的基础上, 在
在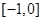 单调递减,在
单调递减,在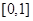 在单调递增
在单调递增
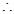 当
当 时,
时, 取得最小值
取得最小值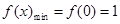
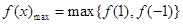 ,进而作差比较大小,得到关于a的函数,结合导数求解得到。
,进而作差比较大小,得到关于a的函数,结合导数求解得到。
解:(Ⅰ) 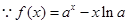 ,∴
,∴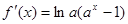 。
。
① 当 时,
时, ,由
,由 可得
可得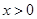 ;由
;由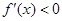 可得
可得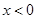
 在
在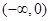 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
②当 时,
时,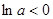 ,由
,由 可得
可得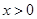 ;由
;由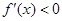 可得
可得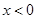
 在
在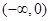 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
综上可得,函数 在
在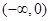 上单调递减,在
上单调递减,在 上单调递增。………4分
上单调递增。………4分
(Ⅱ)由(Ⅰ)知 在
在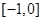 单调递减,在
单调递减,在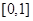 在单调递增
在单调递增
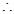 当
当 时,
时, 取得最小值
取得最小值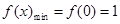
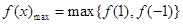 ……………………………………………………6分
……………………………………………………6分
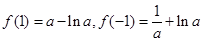 ,
,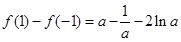
设 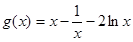 ,则
,则 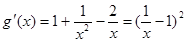 。
。
∵ (当且仅当
(当且仅当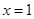 时
时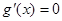 )∴
)∴ 在
在 上单调递增.
上单调递增.
又∵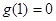 ,
,
∴①当 时,
时,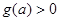 ,即
,即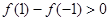 ,
,
这时, 在
在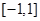 上的最大值为
上的最大值为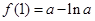 ;
;
②当 时,
时, ,即
,即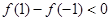
这时, 在
在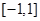 上的最大值为
上的最大值为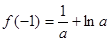 。
。
综上,当 时,
时, 在
在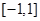 上的最小值为
上的最小值为 ,最大值为
,最大值为 ;
;
当 时,
时, 在
在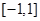 上的最小值为
上的最小值为 ,最大值为
,最大值为 …………12分
…………12分


科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知A、B、C为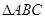 的三个内角且向量
的三个内角且向量 共线。
共线。
(Ⅰ)求角C的大小;
(Ⅱ)设角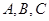 的对边分别是
的对边分别是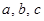 ,且满足
,且满足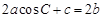 ,试判断
,试判断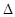
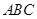 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高三一诊模拟理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装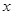 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为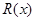 万元,且
万元,且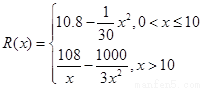 .
.
(I)写出年利润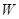 (万元)关于年产量
(万元)关于年产量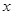 (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源:2013届山东聊城莘县实验高中高二第三次模块测试数学试卷(解析版) 题型:解答题
(本题共12分)
已知函数 ,其中
,其中 且
且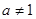 。
。
(Ⅰ)讨论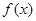 的单调性;
的单调性;
(Ⅱ)求函数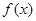 在〔
在〔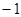 ,
,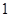 〕上的最小值和最大值。
〕上的最小值和最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com