
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度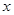 (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当 时,车流速度
时,车流速度 是车流密度x的一次函数.
是车流密度x的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
(Ⅰ)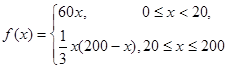 ;(Ⅱ)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
;(Ⅱ)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
解析试题分析:(1)分析可知当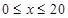 时,车流速度为常数所以此时
时,车流速度为常数所以此时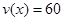 。当
。当 时
时 为一次函数,则可设其方程为
为一次函数,则可设其方程为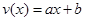 。再根据已知
。再根据已知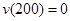 和
和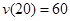 列出方程组求
列出方程组求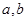 .(2)现根据
.(2)现根据 的解析式求出
的解析式求出 的解析式,所以
的解析式,所以 也是分段函数,需分情况讨论当
也是分段函数,需分情况讨论当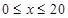 时
时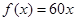 ,此时
,此时 在
在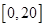 上是增函数,所以
上是增函数,所以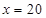 时
时 最大,当
最大,当 时
时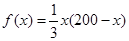 利用基本不等式(或配方法)求最值。最后比较这两个最大值的大小取其中最大的一个
利用基本不等式(或配方法)求最值。最后比较这两个最大值的大小取其中最大的一个
试题解析:(1)由题意:当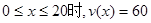 ;当
;当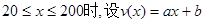
再由已知得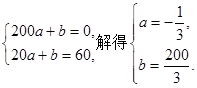
故函数 的表达式为
的表达式为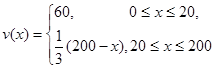
(2)依题意并由(1)可得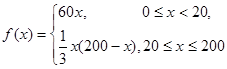
当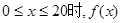 为增函数,故当
为增函数,故当 时,其最大值为60×20=1200;
时,其最大值为60×20=1200;
当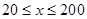 时,
时,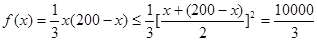
当且仅当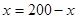 ,即
,即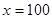 时,等号成立。
时,等号成立。
所以,当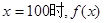 在区间[20,200]上取得最大值
在区间[20,200]上取得最大值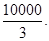 .
.
综上,当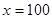 时,
时, 在区间[0,200]上取得最大值
在区间[0,200]上取得最大值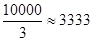
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
考点:(1)函数解析式的求法(2)最值问题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
(1)求证:当 满足条件
满足条件 时,对于
时,对于 ,
,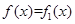 ;
;
(2)设 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若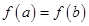 ,求函数
,求函数 在区间
在区间 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“地沟油”严重危害了人民群众的身体健康,某企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为: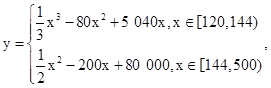
且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径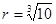 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.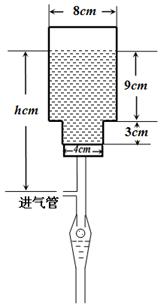
(1)如果瓶内的药液恰好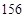 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后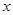 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为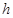 (单位:厘米),已知当
(单位:厘米),已知当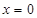 时,
时,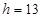 .试将
.试将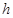 表示为
表示为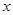 的函数.(注:
的函数.(注: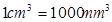 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数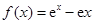 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)求证: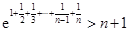
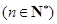 ;
;
(Ⅲ)对于函数 与
与 定义域上的任意实数
定义域上的任意实数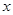 ,若存在常数
,若存在常数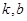 ,使得
,使得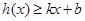 和
和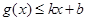 都成立,则称直线
都成立,则称直线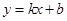 为函数
为函数 与
与 的“分界线”.设函数
的“分界线”.设函数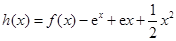 ,
,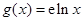 ,
, 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出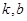 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com