
(Ⅰ)试比较![]() 的大小;
的大小;
(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.
科目:高中数学 来源: 题型:
(08年聊城市二模) (14分) 设关于x的方程![]() 有两个实根α、β,且
有两个实根α、β,且![]() 。定义函数
。定义函数
![]()
(I)求![]() 的值;
的值;
(II)判断![]() 上单调性,并加以证明;
上单调性,并加以证明;
(III)若![]() 为正实数,①试比较
为正实数,①试比较![]() 的大小;
的大小;
②证明![]()
查看答案和解析>>
科目:高中数学 来源:2012届江苏省泰州中学高三上学期期中考试数学 题型:解答题
(本题满分16分)(Ⅰ)试比较 的大小;
的大小;
(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.
查看答案和解析>>
科目:高中数学 来源:2012届甘肃省陇东中学高三第三次模拟考试数学 题型:解答题
(本小题满分12分)
已知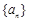 是等比数列,
是等比数列, 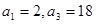 ,
,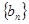 是等差数列,
是等差数列,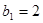
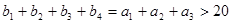
(1)求数列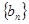 的通项公式;
的通项公式;
(2)求数列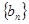 的前n项和
的前n项和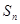 ;
;
(3)设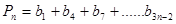 ,
,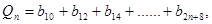 其中n=1,2,......,试比较
其中n=1,2,......,试比较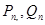 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:2013届辽宁省高二期末教学质量测试理科数学 题型:解答题
已知等差数列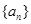 的公差
的公差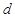 大于0,且
大于0,且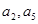 是方程
是方程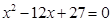 的两根,数列
的两根,数列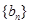 的前
的前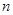 项和为
项和为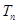 ,且
,且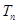
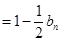
(1)求数列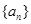 、
、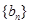 的通项公式;
的通项公式;
(2)设数列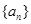 的前
的前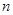 项和为
项和为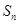 ,试比较
,试比较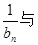
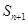 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届山西省高三上学期第二次阶段性测试理科数学 题型:解答题
(本小题满分12分)已知数列 是首项
是首项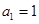 的等差数列,其前n项和为
的等差数列,其前n项和为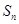 ,
,
数列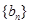 是首项
是首项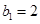 的等比数列,且
的等比数列,且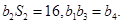
(1)求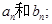
(2)令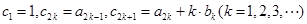 ,若数列
,若数列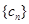 的前n项和为
的前n项和为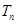 ,试比较
,试比较 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com