
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,比较
,比较![]() 与1的大小关系,并说明理由.
与1的大小关系,并说明理由.
【答案】(1)当![]() 时,函数
时,函数![]() 无极值,当
无极值,当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,无极小值;(2)
,无极小值;(2)![]() ,理由见解析.
,理由见解析.
【解析】
试题分析:(1)依题意![]() ,分子是一个二次项系数含有参数的式子,所以要对
,分子是一个二次项系数含有参数的式子,所以要对![]() 进行分类讨论,根据开口方向,将
进行分类讨论,根据开口方向,将![]() 分成
分成![]() 和
和![]() 两类来讨论函数的单调区间和极值;(2)
两类来讨论函数的单调区间和极值;(2)![]() ,即比较
,即比较![]() 与
与![]() 的大小. 令
的大小. 令![]() ,即比较
,即比较![]() 与
与![]() 的大小.构造函数
的大小.构造函数![]() 利用导数求得其最大值为
利用导数求得其最大值为![]() ,得证.
,得证.
试题解析:
(1)依题意![]()
①若![]() ,则
,则![]() 在
在![]() 上恒成立,函数
上恒成立,函数![]() 无极值;
无极值;
②若![]() ,则
,则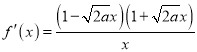 ,此时
,此时![]() ,
,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为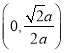 ,单调减区间为
,单调减区间为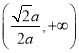 ,
,
故函数![]() 的极大值为
的极大值为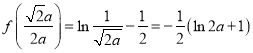 ,无极小值.
,无极小值.
综上所述,当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,无极小值
,无极小值
(2)依题意,![]() ,
,
要比较![]() 与1的大小 ,即比较
与1的大小 ,即比较![]() 与
与![]() 的大小.
的大小.
∵![]() ,∴可比较
,∴可比较![]() 与
与![]() 的大小
的大小
令![]() ,即比较
,即比较![]() 与
与![]() 的大小.
的大小.
设![]() ,
,
则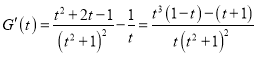 ,
,
因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,所以
,所以![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】某中学高三数学奥林匹克竞赛集训队的一次数学测试成绩的茎叶图(图1)和频率分布直方图(图2)都受到不同程度的破坏,可见部分如图所示,据此解答如下问题.
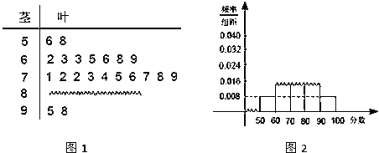
(1)求该集训队总人数及分数在[80,90)之间的频数;
(2)计算频率分布直方图中[80,90)的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生的答题情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年的蔬菜销售收入均为50万元,设![]() 表示前
表示前![]() 年的纯利润总和(
年的纯利润总和(![]() =前
=前![]() 年的总收入
年的总收入![]() 前
前![]() 年的总支出
年的总支出![]() 投资额).
投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:
① 当年平均利润达到最大时,以48万元出售该厂;
② 当纯利润总和达到最大时,以16万元出售该厂,
问哪种方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)若![]() ,存在实数
,存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,侧面
,侧面![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 是
是![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() .
.
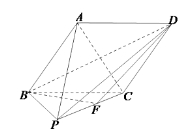
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)若点![]() 在线段
在线段![]() 上移动,是否存在点
上移动,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,指出点
?若存在,指出点![]() 的位置,否则说明理由.
的位置,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 实数
实数![]() 满足不等式
满足不等式![]() 函数
函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com