
【题目】已知单调递减的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4是等差中项,则公比q= , 通项公式为an= .
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+y)=f(x)f(y),且f(1)= ![]() .
.
(1)当n∈N*时,求f(n)的表达式;
(2)设an=nf(n),n∈N* , 求证a1+a2+a3+…+an<2;
(3)设bn=(9﹣n) ![]() ,n∈N* , Sn为bn的前n项和,当Sn最大时,求n的值.
,n∈N* , Sn为bn的前n项和,当Sn最大时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(ωx+φ)(ω>0,|φ|< ![]() )的图象上的每一点的纵坐标不变,横坐标缩短为原来的一半,再将图象向右平移
)的图象上的每一点的纵坐标不变,横坐标缩短为原来的一半,再将图象向右平移 ![]() 个单位长度得到函数y=sinx的图象.
个单位长度得到函数y=sinx的图象.
(1)直接写出f(x)的表达式,并求出f(x)在[0,π]上的值域;
(2)求出f(x)在[0,π]上的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() (
(![]() ),从
),从![]() 上的点
上的点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,再从点
,再从点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() .设
.设![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: 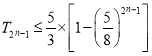 ;
;
(Ⅲ)若已知![]() (
(![]() ),记数列
),记数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图. 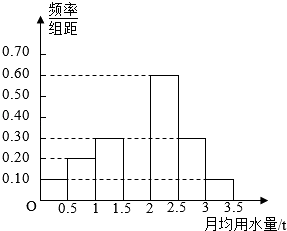
(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准则月均用水量的最低标准定为多少吨,请说明理由;
(3)从频率分布直方图中估计该100位居民月均用水量的众数,中位数,平均数(同一组中的数据用该区间的中点值代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(Ⅰ)证明:CD⊥AE;
(Ⅱ)证明:PD⊥平面ABE;
(Ⅲ)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0,另一边CD所在直线方程为x+3y+7=0,
(Ⅰ)求正方形中心G所在的直线方程;
(Ⅱ)设正方形中心G(x0 , y0),当正方形仅有两个顶点在第一象限时,求x0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,B= ![]() ,AC=2
,AC=2 ![]() ,cosC=
,cosC= ![]() .
. 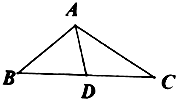
(1)求sin∠BAC的值及BC的长度;
(2)设BC的中点为D,求中线AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com