
【题目】已知![]()
![]() 且
且![]()
(1)求函数![]() 的定义域及其零点;
的定义域及其零点;
(2)若关于![]() 的方程
的方程![]() 在区间[0,1)内有解,求实数
在区间[0,1)内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)定义域为![]() ,零点为0;(2)分类讨论,答案见解析.
,零点为0;(2)分类讨论,答案见解析.
【解析】
(1)求定义域要求真数大于0,列不等式组可得结果,求零点令函数值为0,解方程可在定义域内得函数的零点;
(2)利用函数零点(方程有根)求参数范围问题,可构造新函数,转化为两个函数有交点问题,也可利用函数的单调性,确定参数的取值范围.
解:(1)由![]() 得
得![]() ,
,
故![]() 的定义域为
的定义域为![]() ,
,
由![]() ,即
,即![]() ,
,
得![]() ,
,
得![]() ,
,
解得![]() 或
或![]() ,
,
由于![]() ,故
,故![]() 的零点为0;
的零点为0;
(2)方法一:
![]() 在区间[0,1)内有解,即
在区间[0,1)内有解,即![]() ,
,![]() 有解,
有解,![]()
令![]() ,
,![]() ,
,![]() ,
,![]() 在(0,1]为减函数,
在(0,1]为减函数,
则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ;
;
方法二:
由![]() 方程在区间[0,1)内有解,即
方程在区间[0,1)内有解,即![]() 与
与![]() 在
在![]() 有交点,
有交点,
![]() .令
.令![]() ,
,![]() ,
,![]() ,
,
![]() 在(0,1]为减函数,
在(0,1]为减函数,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ;
;
方法三:
![]() ,
,
当![]() 时,
时,![]() 在[0,1)上为增函数,此时
在[0,1)上为增函数,此时![]() ,故此时
,故此时![]()
当![]() 时,
时,![]() 在[0,1)上为减函数,此时
在[0,1)上为减函数,此时![]() ,故此时
,故此时![]() ,
,
综上![]() 时,
时,![]() ,
,![]() 时
时![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(![]() )(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
)(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
(1)确定b的值;
(2)证明函数y=f(x)在定义域上单调递增,并求a的值;
(3)若对于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: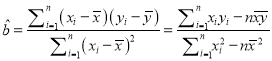 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数.
试问:(1)能组成多少个不同的五位偶数?
(2)五位数中,两个偶数排在一起的有几个?
(3)两个偶数不相邻且三个奇数也不相邻的五位数有几个?(所有结果均用数值表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任意一点到两焦点
上任意一点到两焦点![]() 距离之和为
距离之和为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.点
两点.点![]() 为椭圆上一点,求
为椭圆上一点,求![]() 的面积的最大值及此时直线
的面积的最大值及此时直线![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:

(1)根据表中的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形的勃劳卡德点是以法国军官亨利·勃劳卡德(Henri.Brocard)命名的,他在1875年曾描述过这一事实,即:对任何一个三角形都存在唯一的角![]() ,即勃劳卡德角,使得图中连接三个顶点的线相交于勃劳卡德点Q,如图所示.
,即勃劳卡德角,使得图中连接三个顶点的线相交于勃劳卡德点Q,如图所示.
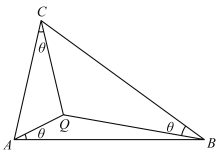
(1)研究发现:等腰直角三角形中![]() ,若
,若![]() 是斜边
是斜边![]() 的等腰直角三角形,求线段
的等腰直角三角形,求线段![]() 的长度;
的长度;
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() 中,若线段
中,若线段![]() ,
,![]() ,
,![]() 的长度是1为首项,公比为q(
的长度是1为首项,公比为q(![]() )的等比数列,当
)的等比数列,当![]() 时,求公比q的值.
时,求公比q的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com