
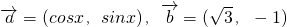
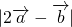 的最大值及相应x的值;
的最大值及相应x的值; •
•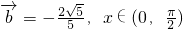 时,求cosx的值.
时,求cosx的值.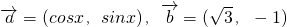
 =
=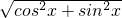 =1,
=1, =
= =2
=2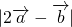 ≤2
≤2 +
+ =4,
=4, 与
与 共线且反向时,即
共线且反向时,即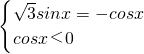 时,等号成立
时,等号成立 +2kπ,k∈Z
+2kπ,k∈Z +2kπ(k∈Z)时,
+2kπ(k∈Z)时,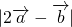 的最大值为4
的最大值为4 •
• =
= cosx-sinx=-
cosx-sinx=-
 )=
)= ,得sin(x-
,得sin(x- )=
)=
 ,得x-
,得x- ∈(-
∈(- ,
, )
) )=
)=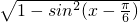 =
=
 )+
)+ ]=
]=
 -
-
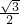 =
=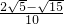
 =1且
=1且 =2,再由向量的三角形不等式得
=2,再由向量的三角形不等式得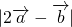 ≤2
≤2 +
+ ,由此不难得到
,由此不难得到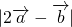 的最大值及相应x的值;
的最大值及相应x的值; )=
)= .再利用配角:x=(x-
.再利用配角:x=(x- )+
)+ ,并结合两角和的余弦公式即可算出cosx的值.
,并结合两角和的余弦公式即可算出cosx的值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届浙江省杭州市高一5月月考数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求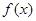 的最大值及取得最大值时的
的最大值及取得最大值时的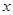 集合;
集合;
(2)设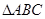 的角
的角 的对边分别为
的对边分别为 ,且
,且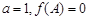 .求
.求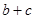 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省增城市高三毕业班调研测试数学理卷 题型:解答题
(本题满分14分)设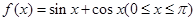
(1)求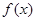 的最大值及
的最大值及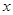 的值;
的值;
(2)求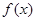 的单调区间;
的单调区间;
(3)若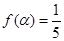 ,求
,求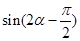 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com