
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(Ⅰ)证明:BE⊥DC;
(Ⅱ)求直线BE与平面PBD所成角的正弦值;
(Ⅲ)若F为棱PC上一点,满足BF⊥AC,求二面角F﹣AB﹣P的余弦值.
【答案】证明:(I)∵PA⊥底面ABCD,AD⊥AB,
以A为坐标原点,建立如图所示的空间直角坐标系,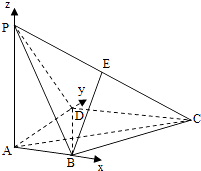
∵AD=DC=AP=2,AB=1,点E为棱PC的中点.
∴B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(1,1,1)
∴ ![]() =(0,1,1),
=(0,1,1), ![]() =(2,0,0)
=(2,0,0)
∵ ![]() =0,
=0,
∴BE⊥DC;
(Ⅱ)∵ ![]() =(﹣1,2,0),
=(﹣1,2,0), ![]() =(1,0,﹣2),
=(1,0,﹣2),
设平面PBD的法向量 ![]() =(x,y,z),
=(x,y,z),
由  ,得
,得 ![]() ,
,
令y=1,则 ![]() =(2,1,1),
=(2,1,1),
则直线BE与平面PBD所成角θ满足:
sinθ= 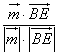 =
= ![]() =
= ![]() ,
,
故直线BE与平面PBD所成角的正弦值为 ![]() .
.
(Ⅲ)∵ ![]() =(1,2,0),
=(1,2,0), ![]() =(﹣2,﹣2,2),
=(﹣2,﹣2,2), ![]() =(2,2,0),
=(2,2,0),
由F点在棱PC上,设 ![]() =λ
=λ ![]() =(﹣2λ,﹣2λ,2λ)(0≤λ≤1),
=(﹣2λ,﹣2λ,2λ)(0≤λ≤1),
故 ![]() =
= ![]() +
+ ![]() =(1﹣2λ,2﹣2λ,2λ)(0≤λ≤1),
=(1﹣2λ,2﹣2λ,2λ)(0≤λ≤1),
由BF⊥AC,得 ![]()
![]() =2(1﹣2λ)+2(2﹣2λ)=0,
=2(1﹣2λ)+2(2﹣2λ)=0,
解得λ= ![]() ,
,
即 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
设平面FBA的法向量为 ![]() =(a,b,c),
=(a,b,c),
由 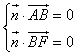 ,得
,得 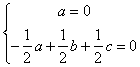
令c=1,则 ![]() =(0,﹣3,1),
=(0,﹣3,1),
取平面ABP的法向量 ![]() =(0,1,0),
=(0,1,0),
则二面角F﹣AB﹣P的平面角α满足:
cosα= ![]() =
= ![]() =
= ![]() ,
,
故二面角F﹣AB﹣P的余弦值为: ![]()
【解析】(I)以A为坐标原点,建立如图所示的空间直角坐标系,求出BE,DC的方向向量,根据 ![]() =0,可得BE⊥DC;(II)求出平面PBD的一个法向量,代入向量夹角公式,可得直线BE与平面PBD所成角的正弦值;(Ⅲ)根据BF⊥AC,求出向量
=0,可得BE⊥DC;(II)求出平面PBD的一个法向量,代入向量夹角公式,可得直线BE与平面PBD所成角的正弦值;(Ⅲ)根据BF⊥AC,求出向量 ![]() 的坐标,进而求出平面FAB和平面ABP的法向量,代入向量夹角公式,可得二面角F﹣AB﹣P的余弦值.
的坐标,进而求出平面FAB和平面ABP的法向量,代入向量夹角公式,可得二面角F﹣AB﹣P的余弦值.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则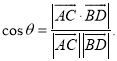 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=2an﹣1(n∈N+),a1=2.
(1)求证:数列{an﹣1}为等比数列,并求数列{an}的通项公式;
(2)求数列{nan}的前n项和Sn(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2(x+ ![]() ),g(x)=1+
),g(x)=1+ ![]() sin2x.
sin2x.
(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(x0)的值.
(2)设函数h(x)=f(x)+g(x),若不等式|h(x)﹣m|≤1在[﹣ ![]() ,
, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程C:x2+y2﹣2x﹣4y+m=0,
(1)若方程C表示圆,求实数m的范围;
(2)在方程表示圆时,该圆与直线l:x+2y﹣4=0相交于M、N两点, ![]() ,求m的值;
,求m的值;
(3)在(2)的条件下,定点A(1,0),P在线段MN上运动,求直线AP的斜率取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(2,0),B(0,2),C(cosα,sinα).
(1)若 ![]() ,且α∈(0,π),求角α的值;
,且α∈(0,π),求角α的值;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2016年11月份人均用电情况进行统计后,按人均用电量分为
位居民2016年11月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
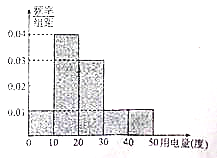
A. 11月份人均用电量人数最多的一组有![]() 人
人
B. 11月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. 11月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件,求直线的方程:
(Ⅰ)过直线l1:2x﹣3y﹣1=0和l2:x+y+2=0的交点,且垂直于直线2x﹣y+7=0;
(Ⅱ)过点(﹣3,1),且在两坐标轴上的截距之和为﹣4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2﹣2(m+3)x+2(1﹣4m2)y+16m4+9=0表示一个圆.
(1)求实数m的取值范围;
(2)求该圆半径r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com