
【题目】已知直线![]() 的方程为
的方程为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(Ⅰ)求过![]() 点且与直线
点且与直线![]() 平行的直线方程;
平行的直线方程;
(Ⅱ)求过![]() 点且与直线
点且与直线![]() 垂直的直线方程.
垂直的直线方程.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】
试题分析:(1)设过P点且与直线l平行的直线方程为x+2y+k=0,把P点坐标代入求得k值得答案;(2)设过P点且与直线l垂直的直线方程为2x-y+b=0,把P点坐标代入求得b值得答案
试题解析::(1)设过P点且与直线l平行的直线方程为x+2y+k=0,…(2分)
则1+2×(-2)+k=0,即k=3,…(3分)
∴过P点且与直线l平行的直线方程为x+2y+3=0…(4分);
(2)设过P点且与直线l垂直的直线方程为2x-y+b=0,…(6分)
则2×1-(-2)+b=0,即b=-4,…(7分)
∴过P点且与直线l垂直的直线方程为2x-y-4=0.…(8分)


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
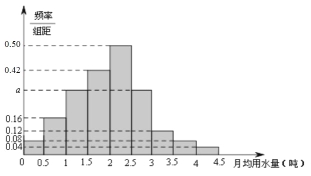
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从数列![]() 中抽出一项,依原来的顺序组成的新叫数列
中抽出一项,依原来的顺序组成的新叫数列![]() 的一个子列.
的一个子列.
(1)写出数列![]() 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)若![]() 是无穷等比数列,首项
是无穷等比数列,首项![]() ,公比
,公比![]() 且
且![]() ,则数列
,则数列![]() 是否存在一个子列,为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
是否存在一个子列,为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程式
的参数方程式 (
(![]() 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,![]() 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组: ![]() ,
,![]() ,
,![]() ,
,![]() ,
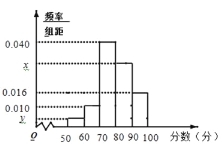
,![]() ,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在
,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 、
、![]() 的值;
的值;
(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知. “![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
, ![]() …
…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
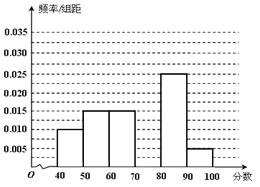
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com