
【题目】已知数列{an}的前n项和为Sn=3n﹣1.
(1)求a1 , a2 , a3的值;
(2)求数列{an}的通项公式;
(3)求数列{nan}的前n项和Tn .
【答案】
(1)解:∵Sn=3n﹣1,
∴a1=3﹣1=2,
a2=S2﹣S1=8﹣2=6,
a3=S3﹣S2=26﹣8=18;
(2)解:∵Sn=3n﹣1,
∴当n≥2时,Sn﹣1=3n﹣1﹣1,
两式相减得:an=23n﹣1,
又∵a1=2满足上式,
∴an=23n﹣1
(3)解:由(2)可知nan=2n3n﹣1,
∴Tn=230+43+632+…+2n3n﹣1,
3Tn=23+432+…+2(n﹣1)3n﹣1+2n3n,
两式相减得:﹣2Tn=2+23+232+…+23n﹣1﹣2n3n,
∴Tn=n3n﹣(1+3+32+…+3n﹣1)
=n3n﹣ ![]()
= ![]() +
+ ![]() 3n
3n
【解析】(1)通过Sn=3n﹣1,直接代入计算即可;(2)通过Sn=3n﹣1与Sn﹣1=3n﹣1﹣1作差,整理即得结论;(3)通过(2)可知nan=2n3n﹣1 , 进而利用错位相减法计算计算即得结论.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系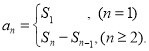 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
,
![]()
![]() 为
为![]() 中点.
中点.

(Ⅰ)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(Ⅱ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,请说明点
,若存在,请说明点![]() 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,l1,l2是通过某城市开发区中心O的两条南北和东西走向的街道,连结M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3 km,点N到l1,l2的距离分别为4 km和5 km.

(1)建立适当的坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4 km,并且铁路线上任意一点到校址的距离不能少于![]() km,求该校址距点O的最近距离.(注:校址视为一个点)
km,求该校址距点O的最近距离.(注:校址视为一个点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆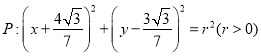 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某渔船在渔港O的南偏东60°方向,距离渔港约160海里的B处出现险情,此时在渔港的正上方恰好有一架海事巡逻飞机A接到渔船的求救信号,海事巡逻飞机迅速将情况通知了在C处的渔政船并要求其迅速赶往出事地点施救.若海事巡逻飞机测得渔船B的俯角为68.20°,测得渔政船C的俯角为63.43°,且渔政船位于渔船的北偏东60°方向上.
(Ⅰ)计算渔政船C与渔港O的距离;
(Ⅱ)若渔政船以每小时25海里的速度直线行驶,能否在3小时内赶到出事地点?
(参考数据:sin68.20°≈0.93,tan68.20°≈2.50,shin63.43°≈0.90,tan63.43°≈2.00, ![]() ≈3.62,
≈3.62, ![]() ≈3.61)
≈3.61)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com