
已知函数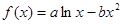 图像上一点
图像上一点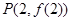 处的切线方程为
处的切线方程为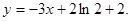 (1)求
(1)求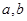 的值;(2)若方程
的值;(2)若方程 在区间
在区间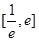 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令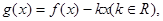 如果
如果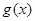 的图像与
的图像与 轴交于
轴交于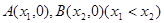 两点,
两点,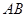 的中点为
的中点为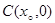 ,求证:
,求证: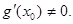
(1) a=2,b=1. (2) 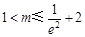 (3)详见解析.
(3)详见解析.
解析试题分析:(1)利用导数几何意义,函数在点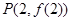 处的导数值为切线的斜率,即
处的导数值为切线的斜率,即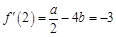 ,又
,又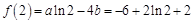 ,所以可得a=2,b=1. (2)利用函数与方程思想,即研究函数
,所以可得a=2,b=1. (2)利用函数与方程思想,即研究函数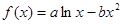 图像与直线
图像与直线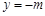 有两个不同的交点,因为
有两个不同的交点,因为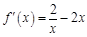 ,所以当x∈
,所以当x∈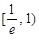 时,
时,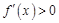 , f(x)是增函数;当x∈
, f(x)是增函数;当x∈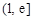 时,
时, 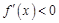 , f(x)是减函数.且
, f(x)是减函数.且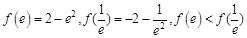 ,所以
,所以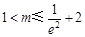 (3)正难则反,假设
(3)正难则反,假设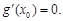 这样从等量关系进行逻辑推理,先列出等量关系
这样从等量关系进行逻辑推理,先列出等量关系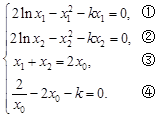 ,五个未知数,四个方程,应建立函数关系,关键是消元,观察可知应消去
,五个未知数,四个方程,应建立函数关系,关键是消元,观察可知应消去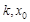 ,得
,得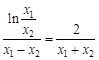 ,转化为
,转化为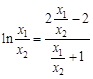 ,这是关于
,这是关于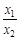 的一元函数
的一元函数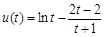 ,利用导数可研究其单调性
,利用导数可研究其单调性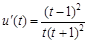 >0,故
>0,故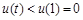 ,即方程无解,假设不成立.
,即方程无解,假设不成立.
试题解析:解:(1)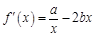 ,
,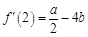 ,
, .
.
∴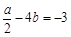 ,且
,且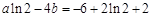 .解得a=2,b=1. . (4分)
.解得a=2,b=1. . (4分)
(2)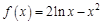 ,设
,设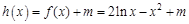 ,
,
则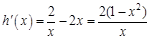 ,令
,令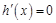 ,得x=1(x=-1舍去).
,得x=1(x=-1舍去).
当x∈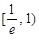 时,
时,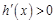 , h(x)是增函数;当x∈
, h(x)是增函数;当x∈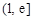 时,
时,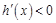 , h(x)是减函数.
, h(x)是减函数.
则方程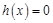 在
在 内有两个不等实根的充要条件是
内有两个不等实根的充要条件是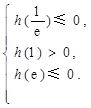 解得
解得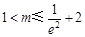 . (8分)
. (8分)
(3)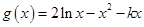 ,
,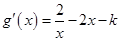 .假设结论
.假设结论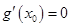 成立,
成立,
则有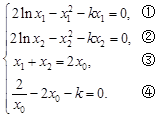 ,①-②,得
,①-②,得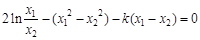 .
.
∴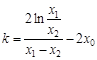 .由④得
.由④得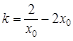 ,于是有
,于是有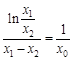 ,∴
,∴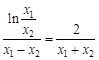 ,
,
即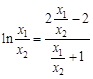 .⑤ 令
.⑤ 令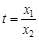 ,
,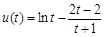 (0<t<1),则
(0<t<1),则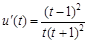 >0.
>0.
∴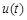 在0<t<1上是增函数,有
在0<t<1上是增函数,有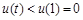 ,∴⑤式不成立,与假设矛盾.
,∴⑤式不成立,与假设矛盾.
∴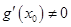 . (12分)
. (12分)
考点:利用导数求切线,利用导数求值域,利用导数证不等式


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率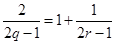
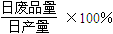 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润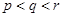 日正品赢利额
日正品赢利额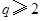 日废品亏损额)
日废品亏损额)
(1)将该车间日利润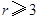 (千元)表示为日产量
(千元)表示为日产量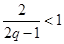 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数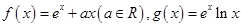 (e为自然对数的底数).
(e为自然对数的底数).
(1)设曲线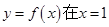 处的切线为
处的切线为 ,若
,若 与点(1,0)的距离为
与点(1,0)的距离为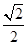 ,求a的值;
,求a的值;
(2)若对于任意实数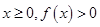 恒成立,试确定
恒成立,试确定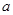 的取值范围;
的取值范围;
(3)当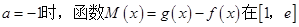 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,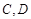 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).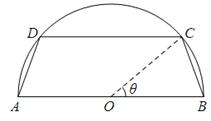
(1)求V关于θ的函数表达式;
(2)求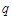 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+ln(x+1).
(1)当a=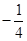 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当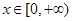 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在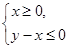 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;
(3)求证: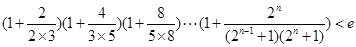 (其中
(其中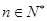 ,e是自然数对数的底数)
,e是自然数对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com