练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    定理：已知O，A，B三点不共线，若点P在直线AB上，且
    OP
    =λ
    OA
    λ2
    OB
    则λ1+λ2=1，类比该定理进行研究，可以得出：已知O、A、B三点不共线，若点P、O在直线AB同侧（点P不在直线AB上），且
    OP
    =λ1
    OA
    λ2
    OB
    ，则
    λ1+λ2＜1
    λ1+λ2＜1
    ．
    分析：延长OP至Q，令OQ在直线AB上，由点P、O在直线AB同侧及向量共线的充要条件可得实数a＜1使得
    OP
    =a
    OQ
    ，又由Q点在直线AB上，可得存在实数μ1，μ2，使
    OQ
    =μ1
    OA
    +μ2
    OB
    且μ1+μ2=1，进而根据λ1+λ2=a（μ1+μ2）得到答案．
    解答：解：延长OP至Q，令OQ在直线AB上，
    则存在实数a使得
    OP
    =a
    OQ
    ，
    ∵P、O在直线AB同侧
    ∴|
    OP
    |    ＜|
    OQ
    |
    ∴a＜1
    又∵则存在实数μ1，μ2，使
    OQ
    =μ1
    OA
    +μ2
    OB
    且μ1+μ2=1
    ∴
    OP
    =λ1
    OA
    +λ2
    OB
    =aμ1
    OA
    +aμ2
    OB

    即λ1+λ2=a（μ1+μ2）＜1
    故答案为：λ1+λ2＜1
    点评：本题又类比推理为载体考查了向量共线的充要条件，向量的基本定理等知识点，熟练掌握向量的基本概念是解答的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013届吉林长春市高二第二次月考文科数学试卷（解析版） 题型：解答题

    已知，如图，AB是⊙O的直径，AC切⊙O于点A，AC=AB，CO交⊙O于点P，CO的延长线交⊙O于点F，   BP的延长线交AC于点E.

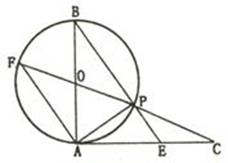
    ⑴求证：FA∥BE；

    ⑵求证：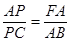

    【解析】本试题主要是考查了平面几何中圆与三角形的综合运用。

    （1）要证明线线平行，主要是通过证明线线平行的判定定理得到

    （2）利用三角形△APC∽△FAC相似，来得到线段成比列的结论。

    证明：（1）在⊙O中，∵直径AB与FP交于点O ∴OA=OF

     ∴∠OAF=∠F  ∵∠B=∠F  ∴∠OAF=∠B ∴FA∥BE

    （2）∵AC为⊙O的切线，PA是弦  ∴∠PAC=∠F

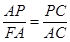
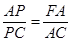    ∵∠C=∠C ∴△APC∽△FAC  ∴

    ∴ ∵AB=AC  ∴

     

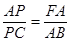
    查看答案和解析>>

    科目：高中数学 来源：吉林省吉林一中2011-2012学年高三阶段验收试题数学 题型：解答题

     

    （理）已知数列{an}的前n项和，且=1，

    .

    （I）求数列{an}的通项公式；

    （II）已知定理：“若函数f(x)在区间D上是凹函数，x>y(x,y∈D)，且f’(x)存在，则有

    < f’(x)”．若且函数y=xn+1在(0,+∞)上是凹函数，试判断bn与bn+1的大小；

    （III）求证：≤bn<2.

    (文)如图，|AB|=2，O为AB中点，直线过B且垂直于AB，过A的动直线与交于点C，点M在线段AC上，满足=.

    （I）求点M的轨迹方程；

    （II）若过B点且斜率为- 的直线与轨迹M交于

             点P，点Q(t,0)是x轴上任意一点，求当ΔBPQ为

             锐角三角形时t的取值范围．

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    定理：已知O，A，B三点不共线，若点P在直线AB上，且
    OP
    =λ
    OA
    λ2
    OB
    则λ1+λ2=1，类比该定理进行研究，可以得出：已知O、A、B三点不共线，若点P、O在直线AB同侧（点P不在直线AB上），且
    OP
    =λ1
    OA
    λ2
    OB
    ，则______．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省泉州市南安三中高三（上）数学模拟试卷（八）（解析版） 题型：填空题

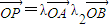    定理：已知O，A，B三点不共线，若点P在直线AB上，且则λ1+λ2=1，类比该定理进行研究，可以得出：已知O、A、B三点不共线，若点P、O在直线AB同侧（点P不在直线AB上），且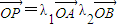，则    ．

    查看答案和解析>>

    同步练习册答案