
【题目】在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() :
:![]() .
.
(1)设![]() 是
是![]() 的左焦点,
的左焦点,![]() 是
是![]() 右支上一点.若
右支上一点.若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)设斜率为1的直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() ;
;
(3)设椭圆![]() :
:![]() .若
.若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,求证:
,求证:![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
【答案】(1)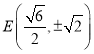 (2)证明见解析(3)证明见解析
(2)证明见解析(3)证明见解析
【解析】
(1)利用![]() ,建立方程,即可求
,建立方程,即可求![]() 点的坐标.
点的坐标.
(2)设直线![]() 的方程为
的方程为![]() ,通过直线
,通过直线![]() 与已知圆相切,得到
与已知圆相切,得到![]() ,通过求解
,通过求解![]() .证明
.证明![]() .
.
(3)当直线![]() 垂直
垂直![]() 轴时,直接求出
轴时,直接求出![]() 到直线
到直线![]() 的距离为
的距离为![]() .当直线
.当直线![]() 不垂直
不垂直![]() 轴时,设直线
轴时,设直线![]() 的方程为:
的方程为:![]() ,(显然
,(显然![]() ),推出直线
),推出直线![]() 的方程为
的方程为![]() ,求出
,求出![]() ,
,![]() ,设
,设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,通过
,通过![]() ,求出
,求出![]() .推出
.推出![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
(1)左焦点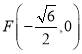 .
.
设![]() ,则
,则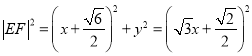 ,
,
由![]() 是右支上一点,知
是右支上一点,知![]() ,所以
,所以![]() ,得
,得![]() .
.
所以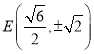 .
.
(2)证明:设直线![]() 的方程是
的方程是![]() .因直线与已知圆相切,
.因直线与已知圆相切,
故![]() ,即
,即![]() .
.
由![]() 与双曲线
与双曲线![]() :
:![]() 联立,得
联立,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]() .
.
所以![]()
![]()
![]() .
.
故![]() .
.
(3)当直线![]() 垂直于
垂直于![]() 轴时,
轴时,
![]() ,
,![]() ,则
,则![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
当直线![]() 不垂直于
不垂直于![]() 轴时,
轴时,
设直线![]() 的方程为
的方程为![]() (显然
(显然![]() ),则直线
),则直线![]() 的方程为
的方程为![]() .
.
由![]() 与椭圆方程联立,得
与椭圆方程联立,得![]() ,
,![]() ,所以
,所以![]() .
.
同理![]() .
.
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为
,因为![]() ,
,
所以 ,即
,即![]() .
.
综上,![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A产品的质量以其质量指标值衡量,质量指标值划分等级及产品售价如下表:
质量指标值m |
|
|
|
产品等级 | 等品 | 二等品 | 三等品 |
售价(每件) | 160元 | 140元 | 120元 |
从该企业生产的A产品中抽取100件作为样本,检测其质量指标值,得到下图的频率分布直方图.
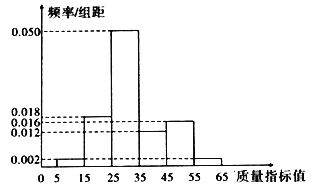
(1)根据频率分布直方图,求A产品质量指标值的中位数;
(2)用样本频率估计总体概率.现有一名顾客随机购买两件A产品,设其支付的费用为X元,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图(![]() )是某品牌汽车
)是某品牌汽车![]() 年月销量统计图,图(
年月销量统计图,图(![]() )是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
)是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
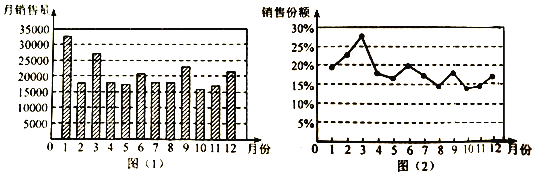
A.该品牌汽车![]() 年全年销量中,
年全年销量中,![]() 月份月销量最多
月份月销量最多
B.该品牌汽车![]() 年上半年的销售淡季是
年上半年的销售淡季是![]() 月份,下半年的销售淡季是
月份,下半年的销售淡季是![]() 月份
月份
C.![]() 年该品牌汽车所属公司
年该品牌汽车所属公司![]() 月份的汽车销量比
月份的汽车销量比![]() 月份多
月份多
D.该品牌汽车![]() 年下半年月销量相对于上半年,波动性小,变化较平稳
年下半年月销量相对于上半年,波动性小,变化较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() .
.
(1)若![]() ,试判断
,试判断![]() 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)对(2)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立,若存在,求出数列
都成立,若存在,求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意的
对任意的![]() ,都有
,都有![]()
![]() ,且
,且![]() ,则称数列
,则称数列![]() 为“k级创新数列”.
为“k级创新数列”.
(1)已知数列![]() 满足
满足![]() 且
且![]() ,试判断数列
,试判断数列![]() 是否为“2级创新数列”,并说明理由;
是否为“2级创新数列”,并说明理由;
(2)已知正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,若
,若![]() ,求数列
,求数列![]() 的前n项积
的前n项积![]() ;
;
(3)设![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,令
,令![]() ,在(2)的条件下,记数列
,在(2)的条件下,记数列![]() 的通项
的通项![]() ,求证:
,求证:![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com