
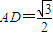
 可得
可得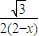 =
=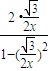 ,解方程求得x的值,即为所求.
,解方程求得x的值,即为所求.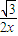 ,tanC=
,tanC= .
.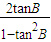 ,∴
,∴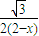 =
= .
. ,解得 x=
,解得 x= 或x=-
或x=- (舍去).
(舍去). .…(7分)
.…(7分)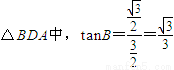 ,则
,则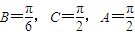 .
.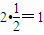 .…(12分)
.…(12分)

科目:高中数学 来源: 题型:
| AB |
| BC |
| π |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
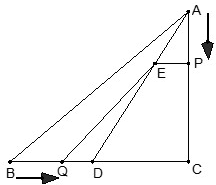 在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为x秒.
在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为x秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com