
如图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,O是点A在平面BCD内的射影.
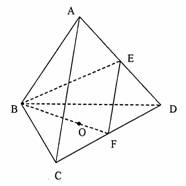
(Ⅰ)求直线EF与直线BC所成角的大小;
(Ⅱ)求点O到平面ACD的距离;
(Ⅲ)求二面角A―BE―F的大小.
方法一:(Ⅰ)因为E、F分别是棱AD、CD的中点,
所以EF∥AC.
所以∠BCA是EF与BC所成角.
∵正四面体ABCD,∴△ABC为正三角形,
所以∠BCA = 60°.即EF与BC所成角的大小是60°
(Ⅱ)解法1:
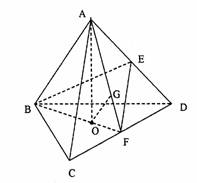
如图,连结AO,AF,
因为F是CD的中点,且△ACD,△BCD均为正三角形,
所以BF⊥CD,AF⊥CD.
因为BF∩AF = F,所以CD⊥面AFB.
因为CD![]() 在ACD,所以面AFB⊥面ACD.
在ACD,所以面AFB⊥面ACD.
因为ABCD是正四面体,且O是点A在面BCD内的射影,
所以点O必在正三角形BCD的中线BF上,
在面ABF中,过O做OG⊥AF,垂足为G,
所以OG⊥在ACD.即OG的长为点O到面ACD的距离.
因为正四面体ABCD的棱长为1,
在△ABF中,容易求出AF = BF=![]() ,OF=
,OF=![]() ,AO =
,AO = ![]() ,
,
因为△AOF∽△OGF,故由相似比易求出OG = ![]()
所以点O到平面ACD的距离是![]()
解法2:

如图,连结AO,CO,DO,
所以点O到平面ACD的距离就是三棱锥O―ACD底面ACD上的高h.
与解法1同理容易求出OF=![]() ,AO =
,AO = ![]() ,
,
所以VA―COD = ![]()
因为VO―ACD = VA―COD,
所以![]() = VO―ACD =
= VO―ACD = ![]() 解得
解得![]()
(Ⅲ)
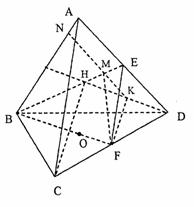
设△ABD中,AB边的中线交BE于H,连结CH,则由ABCD为正四面体知CH⊥面ABD.
设HD的中点为K,则FK∥CH。
所以FK⊥面ABD.
在面ABD内,过点K作KN∥AD,KN交BE于M,交AB于N,
因为BE⊥AD,所以NM⊥BE.
连结FM,所以FM⊥BE.所以∠NMF是所求二面角的平面角.
因为FK = ![]() CH =
CH = ![]() ,MK =
,MK = ![]() ED =
ED = ![]() AD =
AD = ![]() ,
,
所以![]()
所以![]()
所以所求二面角的大小为![]()
(或者由正四面体的对称性,可转求二面角C―BF―E的大小)
方法二:如图,
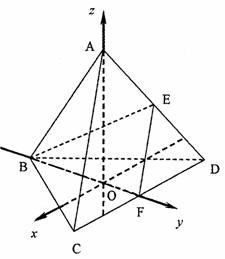
以点A在面BCD的射影O为坐标原点,有向直线OA为z轴,有向直线BF为y轴,x轴为过点O与DC平行的有向直线.
因为正四面体ABCD的棱长为1,所以可以求出各点的坐标依次为:
O(0,0,0),A(0,0,![]() ),B(0,
),B(0,![]() ,0)
,0)
C(![]() ),D(
),D(![]() ),
),
E(![]() ),F(
),F(![]() )
)
(Ⅰ)因为![]()
又![]() ,
,
所以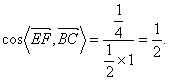 所以EF与BC所成角的大小是60°.
所以EF与BC所成角的大小是60°.
(Ⅱ)因为![]() ,
,
设平面ACD的一个法向量为![]() ,
,
由![]()
因为![]() ,
,
所以点O到平面ACD的距离等于
(Ⅲ)因为![]() ,
,
设平面ABD的一个法向量为![]() ,
,
由![]() ,可得一个法向量
,可得一个法向量![]()
同理可以求出平面BEF的一个法向量为![]()
因为![]()
所以![]()
所以二面角A―BE―F的大小为![]()


科目:高中数学 来源: 题型:
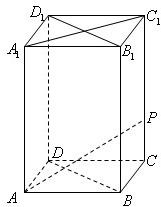 如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.查看答案和解析>>
科目:高中数学 来源: 题型:
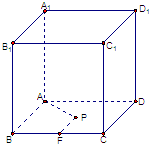 如图:在底面边长为1的正四棱柱ABCD-A1B1C1D1中,P为底面ABCD所在平面内一动点,点P到直线BC的距离等于它到直线AA1的距离,则P点的轨迹方程是( )
如图:在底面边长为1的正四棱柱ABCD-A1B1C1D1中,P为底面ABCD所在平面内一动点,点P到直线BC的距离等于它到直线AA1的距离,则P点的轨迹方程是( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,
(2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•闵行区二模)(文)如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成.
(2009•闵行区二模)(文)如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三下学期期末考试数学试卷 题型:解答题
(本小题满分10分)
如图,在底面边长为1,侧棱长为2的正四棱柱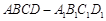 中,P是侧棱
中,P是侧棱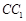 上的一点,
上的一点,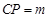 . (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段
. (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段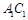 上是否存在一个定点
上是否存在一个定点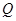 ,使得对任意的m,
,使得对任意的m,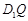 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.
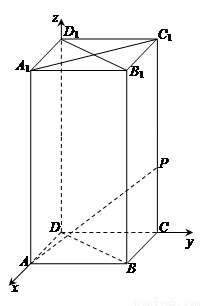
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com