练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】以直角坐标系xOy中，直线l：y=x，圆C： （φ为参数），以坐标原点为为极点，x轴的正半轴为极轴建立极坐标系． （Ⅰ）求直线l与圆C的极坐标方程；
    （Ⅱ）设直线l与圆C的交点为M，N，求△CMN的面积．

    【答案】解：（Ⅰ）将C的参数方程化为普通方程为（x+1）2+（y+2）2=1，极坐标方程为ρ2+2ρcosθ+4ρsinθ+4=0 直线l：y=x的极坐标方程为 （ρ∈R），
    （Ⅱ）圆心到直线的距离d= = ，∴|MN|=2 = ，
    ∴△CMN的面积S= =
    【解析】（Ⅰ）利用三种方程的互化方法，求直线l与圆C的极坐标方程；（Ⅱ）设直线l与圆C的交点为M，N，求出圆心到直线的距离，|MN|，即可求△CMN的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

    (1)求n的值;

    (2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;

    (3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某小学庆“六一”晚会共由6个节目组成，演出顺序有如下要求：节目必须排在前两位，节目不能排在第一位，节目必须排在最后一位，该台晚会节目演出顺序的编排方案共有（ ）

    A. 36种 B. 42种 C. 48种 D. 54种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是公差不为0的等差数列，首项a1=1，且a1 ， a2 ， a4成等比数列． （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设数列{bn}满足bn=an+2 ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： （a＞b＞0）的左焦点为F1（﹣ ，0），e= ． （Ⅰ）求椭圆C的方程；
    （Ⅱ）如图，设R（x0 ， y0）是椭圆C上一动点，由原点O向圆（x﹣x0）2+（y﹣y0）2=4引两条切线，分别交椭圆于点P，Q，若直线OP，OQ的斜率存在，并记为k1 ， k2 ， 求证：k1k2为定值；
    （Ⅲ）在（Ⅱ）的条件下，试问OP2+OQ2是否为定值？若是，求出该值；若不是，说明理由．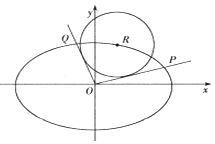

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，.

    （1）求的极值；

    （2） 函数有两个极值点，，若恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了解高三年级学生寒假期间的学习情况，抽取甲、乙两班，调查这两个班的学生在寒假期间每天平均学习的时间（单位：小时），统计结果绘成频率分别直方图（如图）．已知甲、乙两班学生人数相同，甲班学生每天平均学习时间在区间的有8人．

    （I）求直方图中的值及甲班学生每天平均学习时间在区间的人数；

    （II）从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试，设4人中甲班学生的人数为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x），g（x）的定义域都是D，直线x=x0（x0∈D），与y=f（x），y=g（x）的图象分别交于A，B两点，若|AB|的值是不等于0的常数，则称曲线y=f（x），y=g（x）为“平行曲线”，设f（x）=ex-alnx+c（a>0，c≠0），且y=f（x），y=g（x）为区间（0，+）的“平行曲线”，g（1）=e，g（x）在区间（2，3）上的零点唯一，则a的取值范围是_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设k＞0，函数f（x）=+x+kln|x﹣1|．
    （1）讨论函数f（x）的单调性；
    （2）当函数f（x）有两个极值点，且0＜θ＜π时，证明：（2k﹣1）sinθ+（1﹣k）sin[（1﹣k）θ]＞0．

    查看答案和解析>>

    同步练习册答案