
| x4f(2x) |
| ex |
| x4f(2x) |
| ex |
| [x4f(2x)]′ex-x4f(2x)?[ex]′ |
| [ex]2 |
| 4x3f(2x)+2x4f′(2x)-x4f(2x) |
| ex |
| (4x3-x4)f(2x)+2x4f′(2x) |
| ex |
| x3[(4-x)f(2x)+2f′(2x)] |
| ex |
| x4f(2x) |
| ex |
| x4f(2x) |
| ex |
| x4f(2x) |
| ex |


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
| A、c>b>a |
| B、c>a>b |
| C、a>b>c |
| D、a>c>b |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州一中高二下学期期中考试理科数学试卷(带解析) 题型:填空题
给出下列四个结论:① 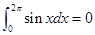 ;
;
②已知集合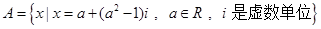 ,若
,若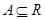 ,则
,则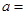 1
1
③已知 为定义在R上的可导函数,且
为定义在R上的可导函数,且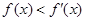 对于
对于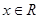 恒成立,则有
恒成立,则有 ,
, 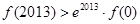 ;
;
④ 若定义在正整数有序对集合上的二元函数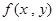 满足:(1)
满足:(1)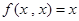 ,(2)
,(2)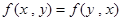 (3)
(3)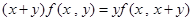 ,则
,则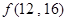 =
=
则其中正确结论的有 (填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
给出下列四个结论:① 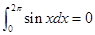 ;
;
②已知集合 ,若
,若 ,则
,则 1
1
③已知 为定义在R上的可导函数,且
为定义在R上的可导函数,且 对于
对于 恒成立,则有
恒成立,则有 ,
,  ;
;
④ 若定义在正整数有序对集合上的二元函数 满足:(1)
满足:(1) ,(2)
,(2) (3)
(3) ,则
,则 =
=
则其中正确结论的有 (填写你认为正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com