分析:(Ⅰ)在矩形C
1D
1DC中,根据勾股定理及其逆定理算出DE⊥EC,再由线面垂直的性质得到DE⊥BC,从而得到DE⊥平面EBC,结合面面垂直判定定理即可证出平面EDB⊥平面EBC;
(II)连接AC交DB于O点,取DD
1的中点F,连接OF.根据平行四边形和三角形中位线定理,可得∠AOF(或其补角)就是异面直线A
1C
1和BD
1所成的角.利用三角形中位线定理和勾股定理,分别算出AF=AO=
,OF=
,最后根据余弦定理算出cos∠FOA,即得A
1C
1和BD
1所成的角的余弦值.
解答:解:(Ⅰ)∵Rt△D
1DE中,DD
1=D
1E=1

∴DE=
=
,同理可得CE=
,
∵DC=2,∴DE
2+CE
2=4=DC
2,可得DE⊥EC
又∵BC⊥平面CC
1D
1D,DE?平面CC
1D
1D,∴DE⊥BC,
∵BC、CE是平面EBC内的相交直线,∴DE⊥平面EBC,
又∵DE?平面EDB,∴平面EDB⊥平面EBC-----------------------(6分)
(Ⅱ)连接AC,交DB于O点,取DD
1的中点F,连接OF,
∵△BDD
1中,O、F分别是BD、DD
1的中点,∴OF∥BD
1,
又∵AC∥A
1C
1,∴∠AOF(或其补角)就是异面直线A
1C
1和BD
1所成的角,----(8分)
Rt△ADF中,AF=
=
,矩形ABCD中,AO=
AC=
=
∵长方体的对角线BD
1=
=
,∴OF=
BD
1=
,----(10分)
∴△AOF中,由余弦定理,得
cos∠FOA=
=
.…(12分)
点评:本题给出特殊长方体,求证面面垂直并求异面直线所成的角,着重考查了线面垂直、面面垂直的判定与性质,异面直线所成角的定义及其求法等知识,属于基础题.

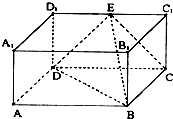 在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连接ED,EC,EB和DB.
在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连接ED,EC,EB和DB.


 名校课堂系列答案
名校课堂系列答案 (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.