
【题目】直线![]() ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0B.![]() C.
C.![]() -1D.
-1D.![]() +1
+1
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】如图,圆![]() ,点
,点![]() ,
,![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线和半径
的垂直平分线和半径![]() 相交于点
相交于点![]() .
.
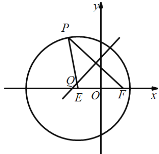
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴上方),且
轴上方),且![]() .点
.点![]() ,
,![]() 是曲线
是曲线![]() 上位于直线
上位于直线![]() 两侧的两个动点,且
两侧的两个动点,且![]() .求四边形
.求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,若对任意的
,若对任意的![]() ,
,![]() ,
,![]() ,存在正数
,存在正数![]() 使得
使得![]() ,则称数列
,则称数列![]() 具有守恒性质,其中最小的
具有守恒性质,其中最小的![]() 称为数列
称为数列![]() 的守恒数,记为
的守恒数,记为![]() .
.
(1)若数列![]() 是等差数列且公差为
是等差数列且公差为![]()
![]() ,前
,前![]() 项和记为
项和记为![]() .
.
①证明:数列![]() 具有守恒性质,并求出其守恒数.
具有守恒性质,并求出其守恒数.
②数列![]() 是否具有守恒性质?并说明理由.
是否具有守恒性质?并说明理由.
(2)若首项为1且公比不为1的正项等比数列![]() 具有守恒性质,且
具有守恒性质,且![]() ,求公比
,求公比![]() 值的集合.
值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;
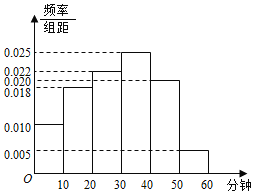
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别有关?
列联表,并据此资料你是否认为“体育迷”与性别有关?
(2)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
附:参考公式:![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
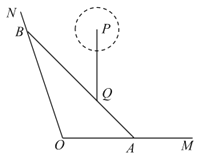
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将
,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将![]() 折起,使得平面
折起,使得平面![]() 平面BDEC(图二).
平面BDEC(图二).

(1)若F是AB的中点,求证:![]() 平面ADE.
平面ADE.
(2)P是AC上任意一点,求证:平面![]() 平面PBE.
平面PBE.
(3)P是AC上一点,且![]() 平面PBE,求二面角
平面PBE,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() 是椭圆
是椭圆![]() 的下顶点,且
的下顶点,且![]() 的周长为6.
的周长为6.

(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 点,证明:当
点,证明:当![]() 变化时,以线段
变化时,以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,
,![]() 是平面内两点,满足
是平面内两点,满足![]() ,线段
,线段![]() 的中点
的中点![]() 在椭圆上,
在椭圆上,![]() 周长为12.
周长为12.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,求
,求![]() (其中
(其中![]() 为坐标原点)的取值范围.
为坐标原点)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求a,b的值;
处具有公共切线,求a,b的值;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围;
内恰有两个零点,求a的取值范围;
(3)![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com