
求由抛物线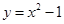 ,直线
,直线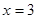 ,
,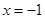 及
及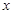 轴所围成的平面图形的的面积
轴所围成的平面图形的的面积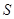
科目:高中数学 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
求由抛物线 与直线
与直线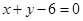 及
及 所围成图形的面积.
所围成图形的面积.
【解析】首先利用已知函数和抛物线作图,然后确定交点坐标,然后利用定积分表示出面积为 ,所以得到
,所以得到 ,由此得到结论为
,由此得到结论为
解:设所求图形面积为 ,则
,则

 =
= .即所求图形面积为
.即所求图形面积为 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com