
已知等比数列 的前
的前 项和为
项和为 ,正数数列
,正数数列 的首项为
的首项为 ,
,
且满足: .记数列
.记数列 前
前 项和为
项和为 .
.
(Ⅰ)求 的值; (Ⅱ)求数列
的值; (Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)是否存在正整数 ,且
,且 ,使得
,使得 成等比数列?若存在,求出
成等比数列?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(Ⅰ)
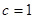 (Ⅱ)
(Ⅱ) 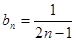
 (Ⅲ) 存在,
(Ⅲ) 存在, 。
。
【解析】熟练掌握并灵活运用等差等比数列的通项公式以及求和公式是解决此题的关键.
(Ⅰ)根据Sn求出a1,a2,a3,根据{an}为等比数列,确定出c的值.
(Ⅱ)根据bn+1=
|
bn |
|
1+2bn |
(n∈N*),得到bn与bn+1的递推关系,根据特殊的数列求通项.
(Ⅲ)先求出Tn,假设满足T1,Tm,Tn成等比数列,得到n与m的关系式,再根据1<m<n,求出m,n的范围,根据m,n是正整数,求出m,n的值.
解:(Ⅰ)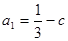 ,
, ,
, ………(3分)
………(3分)
因为 为等比数列所以
为等比数列所以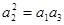 ,得
,得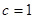 ………………………(4分)
………………………(4分)
经检验此时 为等比数列. ………………(5分)
为等比数列. ………………(5分)
(Ⅱ)∵ 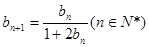 ∴
∴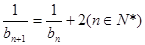
数列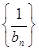 为等差数列 …………………………………………(7分)
为等差数列 …………………………………………(7分)
又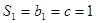 ,所以
,所以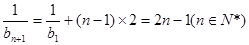
所以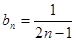
 …………(10分)
…………(10分)
(Ⅲ) ……(12分)
……(12分)
假设存在正整数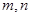 ,且
,且 ,使得
,使得 成等比数列
成等比数列
则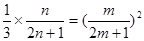 ,所以
,所以
由 得
得 且
且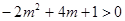
即 ,所以
,所以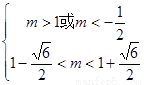
因为 为正整数,所以
为正整数,所以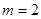 ,此时
,此时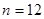
所以满足题意的正整数存在, .…………(15分)
.…………(15分)


科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考文数 题型:解答题
(本题13分)
已知等比数列 的前
的前 项和是
项和是 ,满足
,满足 .
.
(Ⅰ)求数列 的通项
的通项 及前
及前 项和
项和 ;
;
(Ⅱ)若 数列
数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅲ)若对任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市毕业班第四次调研测试文科数学试卷(解析版) 题型:选择题
已知等比数列 的前
的前 项和为
项和为 ,且满足
,且满足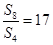 ,则公比
,则公比 =(
)
=(
)
A. B.
B.  C. 2
D.
C. 2
D. 
查看答案和解析>>
科目:高中数学 来源:2013届广东省度高二下学期期中文科数学试卷(解析版) 题型:选择题
已知等比数列{ }的前
}的前 项和为
项和为 ,且
,且 ,则数列
,则数列 的公比
的公比 的值为( )
的值为( )
A. 2 B. 3 C. 2或-3 D. 2或3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com