

图2-5-9
(1)求证:△PBD∽△PEC;
(2)若AB=12,tan∠EAF=![]() ,求⊙O的半径.
,求⊙O的半径.
思路分析:在(1)中,要证相似的两个三角形已经有一个角相等,只要再证其夹边对应成比例即可,而这可由△PAD∽△PEA得到;在(2)中,已知tan∠EAF=![]() ,所以需构造直角三角形,从而运用三角函数求解.
,所以需构造直角三角形,从而运用三角函数求解.
(1)证明:由切割线定理,得PA2=PB·PC.
由△PAD∽△PEA,得PA2=PD·PE,∴PB·PC=PD·PE.
又∠BPD公共,∴△PBD∽△PEC.
(2)解:作OG⊥AB于G,由△PBD∽△PEC可得∠CEP=∠F,
∴PE∥AF.
又OG⊥AB于G,∴AG=![]() AB=6.
AB=6.
∴OG∥ED∥FA.
∴∠AOG=∠EAF.
Rt△AOG中,tan∠AOG=![]() ,又
,又![]() =
=![]() ,∴OG=9.
,∴OG=9.
由勾股定理,AG2+OG2=AO2,∴AO=![]() .
.
∴⊙O半径长为![]() .
.
方法归纳 已知或图形中出现切线、割线等相关的条件时,通常需要借助于切割线定理,以建立线段之间的关系.


科目:高中数学 来源: 题型:
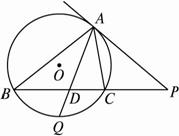
图2-5-9
(1)求证:![]() =
=![]() .
.
(2)若Q为弧BC中点,AQ交BC于D点.求证:![]() =
=![]() .?
.?
查看答案和解析>>
科目:高中数学 来源:2010年陕西省高二第一学期期中考试数学卷 题型:选择题
某商场在国庆黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图1所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为( )
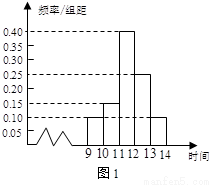
A. 6万元 B. 8万元 C. 10万元 D. 12万元
查看答案和解析>>
科目:高中数学 来源:2010年广东省高二上学期10月月考文科数学卷 题型:选择题
某商场在国庆黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图1所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为( )
A. 6万元 B. 8万元 C. 10万元 D. 12万元

查看答案和解析>>
科目:高中数学 来源: 题型:
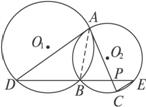
图2-5-11
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com