练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    对于整数，存在唯一一对整数和，使得，. 特别地，当时，称能整除，记作，已知.

    （Ⅰ）存在，使得，试求，的值；

    （Ⅱ）若，（指集合B 中的元素的个数），且存在，，，则称B为“谐和集”.请写出一个含有元素7的“谐和集”和一个含有元素8的非“谐和集”，并求最大的，使含的集合有12个元素的任意子集为“谐和集”，并说明理由.

    【解析】（Ⅰ）因为，所以.   …………………2分

    又因为，所以.          ……………………………4分

    （Ⅱ）含有元素7的一个“和谐集”.…5分

    含有元素8的一个非“和谐集”.…7分

    当时，记，，

    记，则.

    显然对任意，不存在，使得成立. 故是非“和谐集”，此时.

    同理，当时，存在含的集合的有12个元素的子集为非“和谐集”.

    因此.　                 …………………………………………………10分

    下面证明：含7的任意集合的有12个元素的子集为“和谐集”.

    设，若1，14，21中之一为集合的元素，显然为“和谐集” .

    现考虑1，14，21都不属于集合，构造集合，，

    ，，，.…12分

    以上每个集合中的元素都是倍数关系.考虑的情况，也即中5个元素全都是的元素，中剩下6个元素必须从这5个集合中选取6个元素，那么至少有一个集合有两个元素被选，即集合中至少有两个元素存在倍数关系.

    综上，含7的任意集合的有12个元素的子集为“和谐集”，即的最大值为7.    

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2011•朝阳区二模）对于正整数a，b，存在唯一一对整数q和r，使得a=bq+r，0≤r＜b．特别地，当r=0时，称b能整除a，记作b|a，已知A={1，2，3，…，23}．
    （Ⅰ）存在q∈A，使得2011=91q+r（0≤r＜91），试求q，r的值；
    （Ⅱ）求证：不存在这样的函数f：A→{1，2，3}，使得对任意的整数x1，x2∈A，若|x1-x2|∈{1，2，3}，则f（x1）≠f（x2）；
    （Ⅲ）若B⊆A，card（B）=12（card（B）指集合B 中的元素的个数），且存在a，b∈B，b＜a，b|a，则称B为“和谐集”．求最大的m∈A，使含m的集合A的有12个元素的任意子集为“和谐集”，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•朝阳区二模）对于整数a，b，存在唯一一对整数q和r，使得a=bq+r，0≤r＜|b|．特别地，当r=0时，称b能整除a，记作b|a，已知A={1，2，3，…，23}．
    （Ⅰ）存在q∈A，使得2011=91q+r（0≤r＜91），试求q，r的值；
    （Ⅱ）若B⊆A，card（B）=12（card（B）指集合B 中的元素的个数），且存在a，b∈B，b＜a，b|a，则称B为“谐和集”．请写出一个含有元素7的“谐和集”B0和一个含有元素8的非“谐和集”C，并求最大的m∈A，使含m的集合A有12个元素的任意子集为“谐和集”，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于整数，存在唯一一对整数和，使得，. 特别地，当时，称能整除，记作，已知.

    （Ⅰ）存在，使得，试求，的值；

    （Ⅱ）若，（指集合B 中的元素的个数），且存在，，，则称B为“谐和集”.请写出一个含有元素7的“谐和集”和一个含有元素8的非“谐和集”，并求最大的，使含的集合有12个元素的任意子集为“谐和集”，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源：0119 期中题 题型：解答题

    对于正整数a，b，存在唯一一对整数q和r，使得a=bq+r，0≤r＜b。特别地，当r=0时，称b能整除a，记作b|a，已知A={1，2，3，…，23}，
    (1)存在q∈A，使得2011=91q+r（0≤r＜91），试求q，r的值；
    (2)求证：不存在这样的函数f：A→{1，2，3}，使得对任意的整数x，y∈A，若|x-y|∈{1，2，3}，则f（x）≠f（y）；
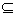    (3)若BA，card（B）=12（card（B）指集合B中的元素的个数），且存在a，b∈B，b＜a，b|a，则称B为“和谐集”。求最大的m∈A，使含m的集合A的有12个元素的任意子集为“和谐集”，并说明理由。

    查看答案和解析>>

    同步练习册答案