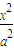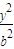练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    双曲线+=1的左焦点为F1，左、右顶点分别为A1、A2，P是双曲线右支上的一点，则分剐以PF1．和A1A2为直径的两圆的位置关系是（ ）
    A．相交
    B．相离
    C．相切
    D．内含
    【答案】分析：取PF1的中点Q，则|OQ|=|PF2|，再由双曲线的定义知，|PF1|+|PF2|=2a．由题意得：两圆的圆心距|OQ|，半径分别为  和 a，化简两圆的圆心距|OQ|，可得两圆的圆心距等于两圆的半径之差．
    解答：解：如图在三角形PF1F2中，取PF1的中点Q，则由三角形中位线大的性质可得
    |OQ|=|PF2|==-a，
    即两圆的圆心距等于两圆的半径之差，
    ∴两圆相内切，
    故选C．
    点评：本题考查圆与圆的位置关系，两圆相内切的充要条件是：两圆的圆心距等于两圆的半径之差．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知双曲线-=1的左焦点为F1,左,右顶点为A1,A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为

    A.相交           B.相切           C.相离              D.以上情况都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线=1的左焦点为F1，左、右顶点为A1、A2，P为双曲线上任意一点，则分别以线段PF1、A1A2为直径的两个圆的位置关系为（    ）

    A.相交          B.相切              C.相离              D.以上情况都有可能

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练19练习卷（解析版） 题型：填空题

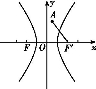
    已知F是双曲线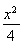-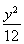=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为　　　　.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河北省衡水市景县中学高二（上）期中数学试卷（解析版） 题型：填空题

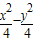    以知F是双曲线=1的左焦点，A（1，4），P是双曲线右支上的动点，则|PF|+|PA|的最小值为    ．

    查看答案和解析>>

    科目：高中数学 来源：2011年高三数学单元检测：圆锥曲线（2）（解析版） 题型：解答题

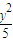    从双曲线-=1的左焦点F引圆x2+y2=3的切线FP交双曲线右支于点P，T为切点，M为线段FP的中点，O为坐标原点，则|MO|-|MT|等于    ．

    查看答案和解析>>

    同步练习册答案