Question

设X是一个56元集合．求最小的正整数n，使得对X的任意15个子集，只要它们中任何7个的并的元素个数都不少于n，则这15个子集中一定存在3个，它们的交非空．  

Answer 1

解析：  n的最小值为41．

首先证明合乎条件．用反证法．假定存在X的15个子集，它们中任何7个的并不少于41个元素，而任何3个的交都为空集．因每个元素至多属于2个子集，不妨设每个元素恰好属于2个子集（否则在一些子集中添加一些元素，上述条件仍然成立），由抽屉原理，必有一个子集，设为A，至少含有＝8个元素，又设其它14个子集为．考察不含A的任何7个子集，都对应X中的41个元素，所有不含A的7－子集组一共至少对应个元素．另一方面，对于元素a，若，则中有2个含有a，于是a被计算了次；若，则中有一个含有a，于是a被计算了次，于是

，

由此可得，矛盾．

其次证明．

用反证法．假定，设，令

，

．

显然，，，

于是,对其中任何3个子集，

必有2个同时为，或者同时为，其交为空集

对其中任何7个子集，有

              

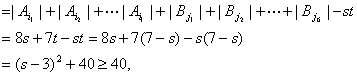
任何3个子集的交为空集，所以n≥41.

综上所述，n的最小值为41．