
【题目】已知函数f(x)=log2(m+![]() )(m∈R,且m>0).
)(m∈R,且m>0).
(1)求函数f(x)的定义域;
(2)若函数f(x)在(4,+∞)上单调递增,求m的取值范围.
【答案】解:(1)由m+![]() >0,(x﹣1)(mx﹣1)>0,
>0,(x﹣1)(mx﹣1)>0,
∵m>0,
∴(x﹣1)(x﹣![]() )>0,
)>0,
若![]() >1,即0<m<1时,x∈(﹣∞,1)∪(
>1,即0<m<1时,x∈(﹣∞,1)∪(![]() ,+∞);
,+∞);
若![]() =1,即m=1时,x∈(﹣∞,1)∪(1,+∞);
=1,即m=1时,x∈(﹣∞,1)∪(1,+∞);
若![]() <1,即m>1时,x∈(﹣∞,
<1,即m>1时,x∈(﹣∞,![]() )∪(1,+∞).
)∪(1,+∞).
(2)若函数f(x)在(4,+∞)上单调递增,则函数g(x)=m+![]() 在(4,+∞)上单调递增且恒正.
在(4,+∞)上单调递增且恒正.
所以 ,
,
解得:![]() .
.
【解析】(1)对数函数要有意义,必须真数大于0,即m+![]() >0,这是一个含有参数的不等式,故对m分情况进行讨论;
>0,这是一个含有参数的不等式,故对m分情况进行讨论;
(2)根据复合函数单调性的判断法则,因为y=log2u是增函数,要使得若函数f(x)在(4,+∞)上单调递增,则函数u=m+![]() 在(4,+∞)上单调递增且恒正,据些找到m满足的不等式,解不等式即得m的范围.
在(4,+∞)上单调递增且恒正,据些找到m满足的不等式,解不等式即得m的范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款iPhone手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在R上可导且满足不等式xf′(x)+f(x)>0恒成立,且常数a,b满足a>b,则下列不等式一定成立的是( )
A.af(a)>bf(b)
B.af(b)>bf(a)
C.af(a)<bf(b)
D.af(b)<bf(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
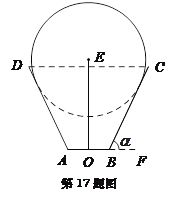
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c,满足f(1)=﹣![]() , 且3a>2c>2b.
, 且3a>2c>2b.
(1)求证:a>0时,![]() 的取值范围;
的取值范围;
(2)证明函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1 , x2是函数f(x)的两个零点,求|x1﹣x2|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个函数:①y=3-x;②y=![]() ;③y=x2+2x-10;④y=-
;③y=x2+2x-10;④y=-![]() .其中值域为R的函数个数有( )
.其中值域为R的函数个数有( )
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.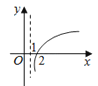
B.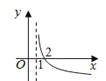
C.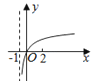
D.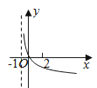
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com