Question

如图,在直三棱柱ABC—A₁B₁C₁中,AA₁=2,AC=BC=1,∠ACB=90°,点E是AB的中点,点F在侧棱BB₁上,且EF⊥CA₁.

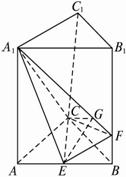
(1)求二面角C-A₁F-E的大小；

(2)求点E到平面CA₁F的距离.

Answer 1

解法一:(1)过E作EG⊥FA₁，垂足为G，连结CG.?

在直三棱柱ABC—A₁B₁C₁中，面A₁B⊥面ABC,?

又AC=BC，E为AB中点,?

∴CE⊥AB.∴CE⊥面A₁B.?

∴CG⊥A₁F.?

∴∠CGE为二面角CA₁FE的平面角.                                                                       ?

又∵CE⊥面A₁B,?

∴CE⊥EF.?

而EF⊥CA₁,∴EF⊥面A₁CE.∴EF⊥A₁E.                                                                ?

∴△A₁AE∽△EBF.?

∴BF=.?

在RT△A₁AE中，A₁E=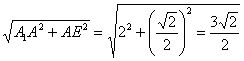.?在RT△EBF中，EF=,

∴A₁F=.?

∴EG=.                                                                       ?

又CE=,?

∴tan∠CGE==1.∴∠CGE=45°,                                                                       ?

即二面角CA₁FE的大小为45°.?

(2)设顶点E到平面A₁CF的距离为d，?

由(1)CG=1，CE⊥面A₁B，A₁F⊥EF，?

V_E—A1CF=V_C—A1EF,?

∴CE·A₁E·EF=×·CG·A₁F·d.?

∴.?

∴d=,

即点E到平面CA₁F的距离为.                                                                                   ?

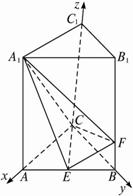
解法二:(1)如图，分别以CA、CB、CC₁为x轴、y轴、z轴建立空间直角坐标系,并设BF=x，则C(0，0，0)，A(1，0，0)，B(0，1，0)，E(，，0)，F(0，1，x)，A₁(1，0，2)，则=(-,,x),=(1,0,2).?

∵EF⊥CA₁，则·=0,?

∴-×1+×0+2x=0,?

x=.∴F(0,1, ).                                                                                                 ?

设向量n=(x,y,z)为平面A₁CF的法向量，则n·=0,

n·=0.?

又=(1,0,2), =(0,1,),∴

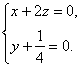
令x=2，则x=-1,y=.∴n=(2,,-1).?

由题意CA=CB，E为AB的中点，∴CE⊥AB.?

又三棱柱ABC—A₁B₁C₁为直三棱柱,?

∴CE⊥平面A₁EF,?

=(,，0)为平面A₁EF的法向量.                                                                  ?

∴Cos〈n,〉=.?

∴〈n,〉=45°.?

∴二面角CA₁FE的大小为45°.                                                                                ?

(2)向量在平面CA₁F的法向量n上的射影的长为d=.?

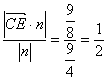向量CE在平面A₁CF的法向量n上的投影长即为点E到平面A₁CF的距离.?

∴点E到平面A₁CF的距离为.                                                                                   ?