
A.1+![]() B.2+
B.2+![]() C.3
C.3![]() D.2
D.2![]()
活动:解决空间几何体表面上两点间最短线路问题,一般都是将空间几何体表面展开,转化为求平面内两点间线段长,这体现了数学中的转化思想.
解:如图3,在长方体ABCD—A1B

图3
如图4所示,将侧面ABB

图4
则有AC1=![]() =
=![]() ,即经过侧面ABB
,即经过侧面ABB![]() ;
;
如图5所示,将侧面ABB
则有AC1=![]() =3
=3![]() ,即经过侧面ABB
,即经过侧面ABB![]() ;
;

图5
如图6所示,将侧面ADD

图6
则有AC1=![]() =2
=2![]() ,即经过侧面ADD
,即经过侧面ADD![]() .
.
由于3![]() <2
<2![]() ,3
,3![]() <
<![]() ,所以由A到C1在正方体表面上的最短距离为3
,所以由A到C1在正方体表面上的最短距离为3![]() .
.
答案:C
点评:本题主要考查空间几何体的简单运算及转化思想.求表面上最短距离可把图形展成平面图形.


科目:高中数学 来源:2012年山东省高考数学预测试卷1(理科)(解析版) 题型:选择题

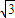
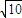
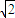
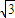
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com