【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且满足 
acosC﹣csinA=0．
（1）求角C的大小；
（2）已知b=4，△ABC的面积为6 ，求边长c的值．
【答案】
（1）解：在△ABC中，由正弦定理得： 
sinAcosC﹣sinCsinA=0． …（2分）
因为0＜A＜π，所以sinA＞0，
从而 cosC=sinC，又cosC≠0，
所以tanC= ，所以C= 
．
（2）解：在△ABC中，S△ABC= 
=6 ，得a=6，
由余弦定理得：c2=62+42﹣2× 
=28，
所以c=2 
【解析】（1）由正弦定理得： sinAcosC﹣sinCsinA=0，即可解得tanC= ，从而求得C的值；（2）由面积公式可得S△ABC= =6 ，从而求得得a的值，由余弦定理即可求c的值．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
，以及对余弦定理的定义的理解，了解余弦定理:
;
;
．
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x（1+m|x|），关于x的不等式f（x）＞f（x+m）的解集记为T，若区间[﹣ 
， ]T，则实数m的取值范围是（ ）
A.（ 
，0）
B.（ 
，0）
C.（﹣∞， ）
D.（ ，0）∪（0， ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，圆
与
轴的正半轴交于点
，以
为圆心的圆
与圆
交于
两点.
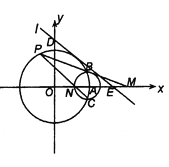
（1）若直线
与圆
切于第一象限，且与坐标轴交于
，当线段
长最小时，求直线
的方程；
（2）设
是圆
上异于
的任意一点，直线
分别与
轴交于点
和
，问
是否为定值？若是，请求出该定值；若不是，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】东莞市某高级中学在今年4月份安装了一批空调，关于这批空调的使用年限
（单位：年， 
）和所支出的维护费用
（单位：万元）厂家提供的统计资料如下：
（1）请根据以上数据，用最小二乘法原理求出维护费用
关于
的线性回归方程
；
（2）若规定当维护费用
超过13.1万元时，该批空调必须报废，试根据（1）的结论预测该批空调使用年限的最大值.
参考公式：最小二乘估计线性回归方程
中系数计算公式：
， 
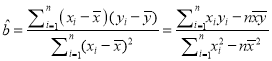，其中
表示样本均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
